Natürliche geometrische Muster oder Muster erscheinen als sich wiederholende Formen, die manchmal durch mathematische Modelle beschrieben oder dargestellt werden können.
Geometrie in der Natur und im Leben gibt es in vielen Formen und Gest alten, wie Symmetrie, Spiralen oder Wellen.
Geschichte
Pythagoras, Empedokles und Plato - erstmals befassten sich antike griechische Philosophen und Wissenschaftler mit Fragen der Geometrie in der Natur. Durch die Analyse von Beispielen vorhersagbarer oder idealer geometrischer Formen bei Pflanzen und Tieren versuchten sie Ordnung und Symmetrie in der Natur zu demonstrieren.
Moderne Versuche, Geometrie in der Natur zu studieren, begannen im 19. Jahrhundert mit den Bemühungen des belgischen Physikers Joseph Plateau, der das Konzept der minimalen Oberfläche einer Seifenblase entwickelte. Die ersten modernen Versuche konzentrierten sich zunächst auf die Demonstration idealer und vorhersagbarer geometrischer Formen und wandten sich dann der Entwicklung von Modellen zu, die das Auftreten und die Manifestation von Geometrie in der Natur vorhersagen.
Im 20. Jahrhundert beschäftigte sich der Mathematiker Alan Turing mit den Mechanismen der Morphogenese, die das Auftreten bei Tieren erklärtverschiedene Muster, Streifen, Flecken. Etwas später wird der Biologe Aristide Lindenmeier zusammen mit dem Mathematiker Benoit Mandelbrot die Arbeit an mathematischen Fraktalen abschließen, die die Wachstumsmuster einiger Pflanzen, einschließlich Bäume, wiederholten.
Wissenschaft
Moderne Wissenschaften (Mathematik, Physik und Chemie) versuchen mit Hilfe von Technologien und Modellen, die in der Natur vorkommenden geometrischen Muster nicht nur zu erklären, sondern auch vorherzusagen.
Die Form und Farbe vieler lebender Organismen wie Pfauen, Kolibris und Muscheln sind nicht nur schön, sondern auch geometrisch korrekt, was die Neugier von Wissenschaftlern weckt. Die Schönheit, die wir in der Natur beobachten, kann natürlich, mathematisch verursacht werden.
Die beobachteten natürlichen Muster in der Mathematik werden durch die Chaostheorie erklärt, die mit Spiralen und Fraktalen arbeitet. Solche Muster gehorchen den Gesetzen der Physik, außerdem sagen Physik und Chemie mithilfe abstrakter Mathematik die Formen natürlicher und künstlicher Kristalle voraus.
Die Biologie erklärt die Geometrie in der Natur durch natürliche Auslese, wobei solche regelmäßigen Merkmale wie Streifen, Flecken, leuchtende Farben durch die Notwendigkeit der Maskierung oder des Sendens von Signalen erklärt werden können.
Arten von Mustern
In der Natur gibt es viele sich wiederholende Muster, die in verschiedenen geometrischen Formen erscheinen. Arten von Grundgesetzmäßigkeiten der Geometrie in der Natur, Fotos und ihre Beschreibungen finden Sie unten.
Symmetrie. Diese geometrische Form ist eine der häufigsten in der Natur. Am häufigsten bei TierenSpiegelsymmetrie - Schmetterlinge, Käfer, Tiger, Eulen. Es kommt auch in Pflanzen wie Ahornblättern oder Orchideenblüten vor. Außerdem kann symmetrische Geometrie in der Natur radial, fünfstrahlig oder sechsfach sein, wie Schneeflocken.

Fraktale. In der Mathematik sind dies selbstähnliche Konstruktionen, die unendlich sind. In der Natur ist es unmöglich, eine solche endlose, sich selbst wiederholende Form zu erkennen, daher werden Annäherungen an fraktale Muster in der Natur als geometrische Fraktale bezeichnet. Eine solche Geometrie kann in der Natur in Farnblättern, Brokkoli, Ananasfrüchten beobachtet werden.
Spiralen. Diese Formen kommen besonders häufig bei Mollusken und Schnecken vor. Wissenschaftler beobachten Spiralformen im Weltraum, zum Beispiel Spiralgalaxien. Die Spirale wird der Goldene Schnitt von Fibonacci genannt.

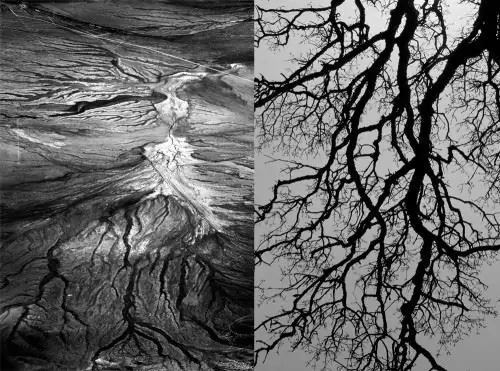
Mäander. Die Zufälligkeit dynamischer Systeme in der Mathematik manifestiert sich in der Natur in Form von Mäandern und Strömungen. Natürliche Geometrie hat die Form einer unterbrochenen oder eher gekrümmten Linie, wie z. B. eines Flusses.
Wellen. Sie werden durch Störungen und Bewegungen der Luft, Windströmungen verursacht, die sich sowohl durch die Luft als auch durch das Wasser ausbreiten. In der Natur sind dies nicht nur Meereswellen, sondern auch Wüstendünen, die geometrische Formen bilden können - Linien, Halbmonde und Parabeln.
Mosaik. Erstellt durch die Wiederholung der gleichen Elemente auf der Oberfläche. Mosaikgeometrie in Wildtieren findet sich in Bienen: Sie bauenBienenstock aus Waben - sich wiederholende Zellen.

Bildung von Mustern
In der Biologie ist die Bildung einer geometrischen Farbe auf den Prozess der natürlichen Selektion zurückzuführen. Bereits Mitte des 20. Jahrhunderts gelang es Alan Turing, den Mechanismus für das Auftreten von Flecken und Streifen in der Farbe von Tieren zu beschreiben - er nannte es das Reaktions-Diffusions-Modell. Bestimmte Körperzellen enth alten Gene, die durch chemische Reaktionen gesteuert werden. Morphogen führt zur Bildung von Hautbereichen mit dunklem Pigment (Flecken und Streifen). Wenn das Morphogen in allen Hautzellen vorhanden ist - wird die Farbe des Panthers erh alten, wenn es ungleichmäßig vorhanden ist - der übliche gefleckte Leopard.






