Unter den Hauptmerkmalen von Karten des Gebiets wird dieses am häufigsten hervorgehoben. Das ist Maßstabsgenauigkeit. In dem Artikel werden wir analysieren, was dieses Konzept in sich verbirgt. Wir werden auch betrachten, was eine Waage im Allgemeinen ist, wir werden ihre Hauptvarianten charakterisieren. Lassen Sie uns analysieren, wie das Konzept der "grafischen Genauigkeit" mit dem Thema unseres Gesprächs zusammenhängt.
Was ist das?
Scale ist eine wichtige Klarstellung, die zeigt, wie viel jede Linie, die auf der Zeichnung, dem Plan, gezeichnet wurde, kleiner oder größer ist als die tatsächliche Größe des Objekts, das sie darstellt. Solche Klarstellungen werden auf Zeichnungsunterlagen und Karten sowohl numerisch als auch grafisch dargestellt.
Planmaßstab, Maßstabsgenauigkeit - Begriffe, die in den unterschiedlichsten Bereichen zu finden sind:
- Kartographie.
- Design.
- Geodäsie.
- Foto.
- Modellierung.
- Programmierung.
- Math.
- Kino.
Einige dieser Anwendungen, ihre Funktionen, werden wir im Laufe des Artikels betrachten.
Skalierungsgenauigkeit
Und jetztDefinition des Schlüsselbegriffs. Maßstabsgenauigkeit - Teil des horizontalen Linienabstands, was in der Zeichnung 0,1 mm bedeutet. Warum wurde dieser Wert gewählt?
0, 1 mm wird hier akzeptiert, da dies das kleinste Segment ist, das vom menschlichen Auge im Bild ohne Verwendung spezieller Geräte, Werkzeuge oder Geräte unterschieden werden kann.
Nehmen wir ein konkretes Beispiel. Gegeben 1:10000. Die Genauigkeit der Waage beträgt jeweils 1 m. Lassen Sie uns genauer analysieren:
- 1 cm auf einem Plan oder Bild sind 10.000 cm (oder 100 m) auf dem realen Gelände.
- 1 mm im Bild sind 1.000 cm (bzw. 10 m).
- 0, 1mm sind 100cm (oder 1m) auf echtem Gelände.
So lässt sich die maximale Genauigkeit der Waage einfach ermitteln. Dies ist der Abstand der realen Oberfläche, gleich 0,1 mm auf der Karte - das kleinste Segment, das eine Person unterscheiden kann.
Grafiktreue
Und jetzt machen wir uns mit der grafischen Genauigkeit von Skalen vertraut. Dies ist ein weiteres wichtiges Merkmal bei der Verwendung von Plänen und Karten.
Graphische Genauigkeit ist mit der Auflösung "und" des menschlichen Auges verbunden. Im Gegenzug macht es "G". Also G=u.
Das heißt, wenn der Winkel "und" zwischen den Vektoren in zwei Punkte "B" und "L" bei Betrachtung durch einen Beobachter mit normalem Sehvermögen "G" oder mehr beträgt, dann werden sie wahrgenommen als zwei Punkte. Wenn dieser Winkel zum Auflösungskonzept kleiner als "G" ist, werden "L" und "B" von einer Person als eins wahrgenommenPunkt.
Machen Sie sich am besten an einem konkreten Beispiel mit der Definition der Waagengenauigkeit vertraut. Nehmen wir an, eine Person untersucht die Karte aus der besten Entfernung "b", gleich 35 cm. Der Wert von G=u. Jetzt müssen Sie den kleinsten Abstand (also die grafische Genauigkeit) zwischen „B“und „L“bestimmen, bei dem sie vom Betrachter noch als zwei verschiedene Punkte wahrgenommen werden. Hier ist die Berechnung:
1 - ist! - 1/3438 x 350 mm=0,1 mm.
1/3438 ist der Wert des Winkels u=r, der in diesem Fall im Bogenmaß ausgedrückt wird (3438' ist die Anzahl der Minuten im Bogenmaß).
Der Ausgabewert von 0,1 mm ist also die grafische Genauigkeit des Plans oder der Karte.
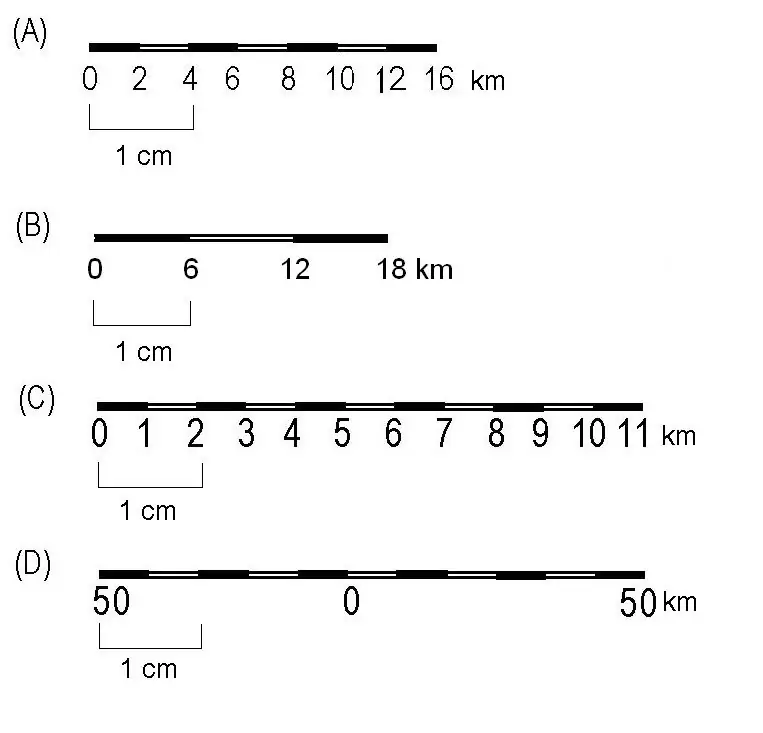
Verbindung von Begriffen
Sehen wir uns nun an, wie sich der obige Begriff auf den Hauptbegriff bezieht. Die Genauigkeit der Skala ist, wie wir uns erinnern, die Entfernung auf der Erdoberfläche, die auf dem Dokument 0,1 mm entspricht.
Du kannst die Formel herleiten:
T=gM=0.1 M mm.
Entschlüssele seine Elemente:
- T - Waagengenauigkeit.
- M ist der Skalennenner.
- r=0,1 mm - grafische Genauigkeit.
Hieraus können wir die entsprechende Interpretation ableiten. Maßstabsgenauigkeit - grafische Genauigkeit, die im Maßstab einer Karte oder eines Plans ausgedrückt wird. Und was ist das Ergebnis? Die grafische Genauigkeit wird für alle vorhandenen Skalen zu einer Konstante (0,1 mm).
Damit ändert sich auch die Waagengenauigkeit. Sie wird umso höher, je größer der Compiler die Skala gewählt hat.
Und jetztwir werden uns mit den Eigenschaften eines solchen Merkmals wie Skala in verschiedenen Anwendungsbereichen befassen.
Design, Geodäsie und Kartographie
Wir wissen, was die "500"-Skalengenauigkeit bedeutet - 1:500. Betrachten wir nun, welche Spielarten davon für den Bereich Design, Kartographie und Geodäsie typisch sind:
- Numerische Skala. Der Indikator wird als Bruch geschrieben. Sein Zähler wird eins sein und sein Nenner wird ein gewisses Maß an Projektionsreduktion auf der Karte sein. Nehmen wir zum Beispiel einen Maßstab von 1:5000. Das bedeutet, dass 1 cm auf einer Karte 5000 cm (oder 50 m) auf einem realen Gelände entspricht. Dementsprechend wird es einen größeren Maßstab geben, der einen kleineren Nenner hat. 1:1.000 ist also größer als 1:20.000.
- Benannte Skala. Der Ersteller der Karte schreibt auf dem Dokument vor, welcher Abstand auf dem realen Gelände 1 cm auf dem Plan entspricht. Hier ein Beispiel: „In 1 Zentimeter sind 1000 Kilometer“. Oder kurz: "1 cm=100 km".
- Grafische Skala. Es wird wiederum in quer und linear unterteilt. Wir werden sie separat analysieren.

Varietäten der grafischen Kategorie
Wie genau ist die Waage - die Querskala? Machen wir uns mit den Eigenschaften vertraut:
- Linear. Ein solcher grafischer Maßstab auf der Karte wird als Lineal dargestellt, das in reelle Teile geteilt wird.
- Quer. Dies ist eine als Nomogramm dargestellte grafische Skala. Seine Konstruktion basiert auf der Proportionalität der Teile paralleler Linien, die die Seiten des Winkels schneiden. Diese Skala dient zur genaueren Messung der Linienlänge auf den Plänen. Sie verwenden es auf diese Weise: Sie messen die Länge auf der unteren Linie einer bestimmten Querskala, so dass das rechte Ende eine ganze Distanz (OM) hat und das linke jenseits von 0 liegt. Wenn in diesem Fall das linke Bein ist zwischen den Zehnteln des linken Segments (ab 0), dann hebt der Spezialist beide Beine des Meters an. Bis sich der linke Schenkel des Messgeräts bereits am Schnittpunkt einer horizontalen Linie und einer beliebigen Querlinie befindet. Aber auch das rechte Bein sollte auf dieser horizontalen Linie liegen. Die minimale CD beträgt hier 0,2 mm. Dementsprechend beträgt die kleinste Genauigkeit 0,1 mm.
Reihe von Bildskalen im Design
Wir wissen bereits, was Präzision im Maßstab 1:500 bedeutet. Aber in welchen Fällen wählt der Compiler es aus? Lassen Sie uns diese Frage analysieren:
- Herunterskalieren. Dementsprechend werden sie in Fällen verwendet, in denen es erforderlich ist, ein Objekt auf einem Plan darzustellen, ein Gelände, das es flächenmäßig erheblich übersteigt. Wendet sich der Ersteller der Gest altung von Masterplänen mit besonders großen Abmessungen zu, muss er die folgenden Maßstäbe verwenden: 1:2.000, 1:5.000, 1:10.000, 1:20.000, 1:25.000, 1:50.000.
- Tatsächliche Größe. Wenn Sie das Objekt auf dem Plan „so wie es ist“darstellen wollen, dann beziehen Sie sich auf den Maßstab „eins zu eins“. Dementsprechend entspricht hier 1 cm realer Länge 1 cm Länge auf dem Plan.
- WaageVergrößerung. Notwendig in Fällen, in denen ein Objekt dargestellt werden muss, das auf dem Plan zu klein ist, um sich ausführlich mit seinem Aussehen und Gerät vertraut zu machen.
Auf Foto
Natürlich ist die Genauigkeit im Maßstab 1:10.000 eher mit Kartographie verbunden. Aber das gilt auch für die Welt der Fotografie. Der Maßstab bedeutet hier das Verhältnis der sogenannten linearen Abmessungen des auf einer hochempfindlichen Matrix oder auf einem fotografischen Film erh altenen Bildes zur Größe der Projektion der entsprechenden Projektionszone auf eine Ebene, die senkrecht zur Kamera steht.
Es gibt Fotografen, die den Maßstab als Verhältnis der Größe eines realen Objekts zu seiner Größe auf einem Bildschirm, Fotopapier oder anderen Medien messen. Aber wie man den Maßstab in einem Foto richtig bestimmt, hängt nur vom Kontext ab, in dem das Bild verwendet wird.
In der Fotografie ist der Maßstab auch wichtig, wenn die Tiefe eines scharf abgebildeten Objekts, des Raums, berechnet wird. Heutzutage haben Spezialisten Zugriff auf eine sehr breite Palette von Maßstäben von unendlich klein (verwendet bei der Aufnahme entfernter Himmelskörper) bis sehr groß (ohne Verwendung spezieller optischer Vorsätze ist es beispielsweise heute möglich, ein Bild im Maßstab 10:1 zu erh alten).
Unter Makrofotografie versteht man hier bereits Aufnahmen im Maßstab 1:1 (und entsprechend größer). Doch mit der Verbreitung digitaler Kompaktkameras wird Makrofotografie auch als Stilrichtung bezeichnet, bei der das Objektiv zu nah an das Motiv herangeführt wird. Betrachtet man also die klassische Definitioneine solche Interpretation wäre nicht korrekt.
In der Modellierung
Für jede Art von Bank- (oder Skalen-) Modellierung werden eigene Skalen definiert. Sie bestehen aus mehreren Skalen, die durch einen gewissen Reduktionsgrad gekennzeichnet sind. Interessanterweise gibt es für jede Art des Modellbaus (Eisenbahn-, Automobil-, Schiffs-, Militär-, Flugzeugmodellbau) bestimmte historisch entstandene maßstabsgetreue Serien, die sich nicht mit anderen überschneiden.
Hier wird die Skala nach einer einfachen Formel berechnet:
L / M=X.
Entziffern:
- L - ursprüngliche Parameter.
- M - Maßstab für die Arbeit erforderlich.
- X ist der gewünschte Wert.
In Programmierung
In diesem Bereich wird die sogenannte Zeitskala wichtig sein. Lassen Sie uns herausfinden, was es ist.
In einem Timesharing-Betriebssystem ist es sehr wichtig, bestimmte Aufgaben in "Echtzeit" auszuführen. Es unterscheidet sich dadurch, dass die Verarbeitung externer Ereignisse ohne zusätzliche Verzögerungen oder Lücken erfolgt. Hier wird ein weiteres Konzept wichtig sein - "Echtzeitskala". Aber es sollte verstanden werden, dass es keinen direkten Bezug zum Maßstab auf den Karten hat. Dies ist nur eine terminologische Konvention.
In der Filmtechnik
In der Filmtechnik kommt es auch auf die Genauigkeit der Zeitskala an. Letzteres ist ein quantitativer Indikator für die Verlangsamung oder Beschleunigung der Bewegung, der dem Verhältnis der Projektionsbildrate zur Aufnahmerate entspricht.
Betrachten Sie dies in einfachen WortenBeispiel. Die Projektionsbildrate für Filmaufnahmen beträgt 24 fps. Die Dreharbeiten wurden gleichzeitig "mit einer Geschwindigkeit" von 72 Bildern / Sek. durchgeführt. Die Zeitskala ist in diesem Fall 1:3.
Und was bedeutet zum Beispiel 2:1? Dies ist doppelt so schnell wie der Standardfluss dessen, was auf dem Bildschirm passiert.
In Mathematik
Skala bezieht sich in diesem Bereich auf die lineare Beziehung zweier Dimensionen. In vielen praktisch anwendbaren Bereichen wird dies auch das Verhältnis der Bildgröße zur tatsächlichen Größe des Bildes sein.
In der Mathematik ist der Maßstab das Verhältnis einer beliebigen Entfernung auf der Karte zur tatsächlichen Entfernung auf dem tatsächlichen Gelände. Wenn wir uns das Beispiel ansehen, ist das dasselbe wie in der Kartographie. Sagen wir 1:100 000 000. 1 cm im Bild entspricht also 100 000 cm in Wirklichkeit. Das heißt, tausend Meter oder ein Kilometer.
Scale ist ein weithin anwendbares Merkmal. Dies ist ein Standard- und integraler Bestandteil bei der Entwicklung von Plänen, Zeichnungen von Objekten, Karten des Gebiets. Es wird im Entwerfen, in der Geodäsie, der Kartographie, in der Fotografie, der Filmtechnik, der Programmierung und der Mathematik verwendet. Es selbst zeichnet sich hauptsächlich durch Genauigkeit aus - das Verhältnis der tatsächlichen Entfernung zur akzeptierten auf der Karte.






