Pyramide zusammen mit einem Prisma ist ein perfektes Polyeder im dreidimensionalen Raum, ihre geometrischen Eigenschaften werden in der High School studiert. In diesem Artikel werden wir betrachten, was Pyramiden sind, aus welchen Elementen sie bestehen, und auch kurz die richtigen Pyramiden charakterisieren.
Geometrische Figur Pyramide
Geometrisch gesehen ist die Pyramide eine räumliche Figur, bestehend aus einem Vieleck und mehreren Dreiecken. Diese Zahl zu bekommen ist ganz einfach. Nehmen Sie dazu ein Polygon mit n Seiten, wählen Sie dann einen beliebigen Punkt im Raum, der nicht in der Ebene des Polygons liegen soll, und verbinden Sie jeden Eckpunkt des Polygons mit diesem Punkt. Offensichtlich wird die so gebildete Figur n Dreiecke haben, die an einer Ecke miteinander verbunden sind.
Um die geometrische Form der beschriebenen Figur zu veranschaulichen, machen wir ein Foto.

Dies zeigt eine viereckige Pyramide, deren Basis istViereck, und die Seitenfläche wird von vier Dreiecken gebildet, die eine gemeinsame Spitze haben.
Pyramidenelemente
Wie jeder Polyeder besteht die Pyramide aus drei Arten von Elementen:
- Kanten;
- tops;
- Rippen.
Gesichter sind Teile von Ebenen, die das innere Volumen einer Figur vom umgebenden Raum trennen. Wenn die Basis der Pyramide ein n-Eck enthält, dann ist die Anzahl ihrer Flächen immer n+1. Davon sind n Seiten dreieckig und eine Seite ist die erwähnte n-eckige Basis.
Vertices sind Punkte, an denen sich drei oder mehr Flächen einer Figur schneiden. Der Basisbereich enthält n Eckpunkte, von denen jeder durch zwei Dreiecksflächen und eine Basis gebildet wird. Der Punkt, an dem sich n Dreiecksseiten treffen, wird als Spitze der Pyramide bezeichnet. Die betrachtete Figur besteht also aus n+1 Ecken.
Kanten sind gerade Linien, die erscheinen, wenn sich zwei Flächen schneiden. Jede Kante ist an ihren Enden durch zwei Scheitelpunkte begrenzt. Jede Pyramide mit einer n-Eck-Basis enthält 2n Kanten. Die Hälfte dieser Zahl, also n, wird allein durch den Schnittpunkt seitlicher Dreiecke gebildet.
Mögliche Figurentypen
Der Name der betrachteten Figur wird eindeutig durch die Art des Polygons an der Basis bestimmt. Wenn sie zum Beispiel drei Ecken und drei Seiten hat, dann ist die Pyramide dreieckig, wenn sie vier ist - viereckig und so weiter.
Polygone können konvex und konkav sowie normal und allgemein sein. All dies bestimmt auch das Aussehen der Pyramide.
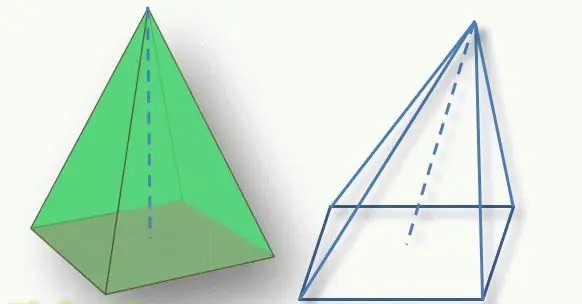
Ein wichtiger Punkt bei der Bestimmung des Figurentyps ist die Position der Spitze der Pyramide relativ zu ihrer Basis. Das senkrechte Segment, das von oben zur polygonalen Basis gezogen wird, wird als Höhe der Figur bezeichnet. Wenn dieses Segment die Basis in ihrem geometrischen Mittelpunkt schneidet (bei einem Dreieck ist dies der Schnittpunkt der Seitenhalbierenden, bei einem Viereck der Schnittpunkt der Diagonalen), wird die Figur als gerade Linie bezeichnet. Ansonsten spricht man von einer schiefen Pyramide.
Wenn das n-Eck der Grundfläche regelmäßig ist (gleichseitiges Dreieck, Quadrat usw.) und die Figur gerade ist, dann spricht man von einer regelmäßigen Pyramide.
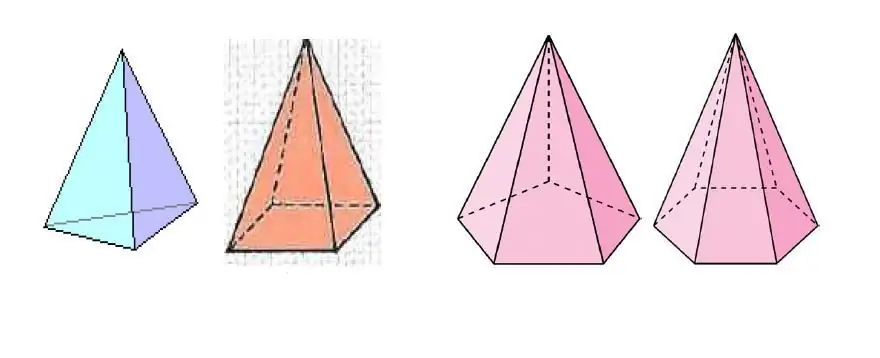
Das obige Bild zeigt mehrere Pyramiden, die sich in der Anzahl der Seiten des Polygons an der Basis unterscheiden.
Eigenschaften regelmäßiger Pyramiden
Diese Pyramiden unterscheiden sich von anderen Figuren dieser Gattung durch ein hohes Maß an Symmetrie. Diesbezüglich lassen sich mit ihnen bequem verschiedene geometrische Berechnungen durchführen, zum Beispiel Volumen oder Oberfläche.
Eine regelmäßige Pyramide enthält an ihrer Basis ein n-Eck, dessen Fläche eindeutig aus der Kenntnis ihrer Seitenlänge bestimmt wird. Die Seitenfläche der Figur wird von n identischen Dreiecken gebildet, die gleichseitig sind. Die Kanten einer regelmäßigen Pyramide, die sich auf der Seitenfläche befindet, sind einander gleich. Der Wert der Länge dieser Kante wird oft zur Berechnung des Apothems einer Figur und zur Bestimmung der Oberfläche verwendet.
Die Höhe einer regelmäßigen Pyramide ist das zweite wichtige Merkmal der Figur (das erste ist die KantenlängeGründen). Die Höhe wird zur Berechnung des Volumens verwendet.
Jede zur Basis parallele Ebene, die die Seitenflächen der Pyramide schneidet, führt zur Bildung eines polygonalen Abschnitts. Es ist bezüglich des Basispolygons homothetisch. Die beschriebene Slice-Operation führt zur Bildung einer ganzen Klasse neuer Figuren - abgeschnittener regelmäßiger Pyramiden.
Die berühmtesten Pyramiden

Natürlich sind dies die regelmäßigen viereckigen Pyramiden der ägyptischen Pharaonen. An einem Ort namens Gizeh gibt es mehr als 100 dieser Steinmonumente, deren perfektes Design und die Genauigkeit der geometrischen Parameter die Wissenschaftler bis heute in Erstaunen versetzen. Die größte von ihnen ist die Cheops-Pyramide, die etwa 146 Meter hoch und etwa 230 Meter lang ist.
Wozu genau diese Pyramiden dienten, nach welchen Mechanismen und wann sie gebaut wurden, weiß bis heute niemand.






