Die Titius-Bode-Regel (manchmal einfach Bodesches Gesetz genannt) ist die Hypothese, dass sich Körper in einigen Orbitalsystemen, einschließlich der Sonne, in Abhängigkeit von der Planetenfolge entlang Halbachsen drehen. Die Formel legt nahe, dass jeder Planet, wenn er sich nach außen erstreckt, etwa doppelt so weit von der Sonne entfernt ist wie der vorherige.
Die Hypothese sagte die Umlaufbahnen von Ceres (im Asteroidengürtel) und Uranus korrekt voraus, konnte aber die Umlaufbahn von Neptun nicht bestimmen und wurde schließlich durch die Theorie der Entstehung des Sonnensystems ersetzt. Es ist nach Johann Daniel Titius und Johann Elert Bode benannt.

Ursprünge
Die erste Erwähnung einer Reihe, die sich dem Bodeschen Gesetz annähert, findet sich in David Gregorys Elements of Astronomy, veröffentlicht 1715. Darin sagt er: „… angenommen, dass die Entfernung von der Sonne zur Erde in zehn gleiche Teile geteilt wird, von denen die Entfernung von Merkur etwa vier, von Venus sieben, von Mars fünfzehn, von Jupiter zweiundfünfzig sein wird, und von Saturn fünfundneunzig . Ein ähnlicher Vorschlag, wahrscheinlich inspiriert von Gregory, erscheint in einem Werk, das 1724 von Christian Wolff veröffentlicht wurde.
Im Jahr 1764 sagte Charles Bonnet in seinem Buch Contemplation of Nature: „Wir kennen die siebzehn Planeten, aus denen unser Sonnensystem besteht [d. h. die Hauptplaneten und ihre Satelliten], aber wir sind uns dessen nicht sicher sie sind nicht mehr." Dazu fügte Johann Daniel Titius in seiner Übersetzung von Bonnets Werk von 1766 zwei eigene Absätze unten auf Seite 7 und oben auf Seite 8 hinzu. Der neue interpolierte Absatz findet sich nicht in Bonnets Origin altext: auch nicht im Italienischen noch englische Übersetzungen der Arbeit.
Entdeckung von Titius
Der interkalierte Text von Titius besteht aus zwei Teilen. Die erste erklärt die Abfolge der planetarischen Entfernungen von der Sonne. Es enthält auch ein paar Worte über die Entfernung von der Sonne zum Jupiter. Aber das ist noch nicht das Ende des Textes.
Es lohnt sich, ein paar Worte zur Formel der Titius-Bode-Regel zu sagen. Achten Sie auf die Abstände zwischen den Planeten und finden Sie heraus, dass fast alle in einem Verhältnis voneinander getrennt sind, das ihrer Körpergröße entspricht. Teilen Sie die Entfernung von der Sonne zum Saturn durch 100 Teile; dann ist Merkur durch vier solche Teile von der Sonne getrennt; Venus - in 4 + 3=7 solcher Teile; Erde - durch 4 + 6=10; Mars - durch 4+12=16.
Aber beachten Sie, dass es von Mars bis Jupiter eine Abweichung von dieser so präzisen Progression gibt. Vom Mars aus folgt ein Raum von 4+24=28 solcher Teile, aber bisher wurde dort kein einziger Planet entdeckt. Aber sollte der Lord Architect diesen Ort leer lassen? Auf keinen Fall. Sonehmen wir an, dass dieser Raum ohne Zweifel zu den noch unentdeckten Monden des Mars gehört, und fügen hinzu, dass Jupiter vielleicht noch ein paar kleinere Monde um sich herum hat, die noch von keinem Teleskop gesehen wurden.

Aufstieg der Bode
1772 vollendete Johann Elert Bode im Alter von 25 Jahren die zweite Auflage seines astronomischen Kompendiums „Anleitung zur Kenntnis des gestirnten Himmels“, zu dem er folgende Fußnote hinzugefügt, ursprünglich ohne Quelle, aber in späteren Versionen vermerkt. In Bodes Memoiren findet sich ein Hinweis auf Titius mit einer klaren Anerkennung seiner Autorität.

Meinung Bode
So klingt die Titius-Bode-Regel in der Darstellung des letzteren: Nimmt man den Abstand von Sonne zu Saturn gleich 100, dann ist Merkur durch vier solche Teile von der Sonne getrennt. Venus - 4+3=7. Erde - 4+6=10. Mars - 4+12=16.
Jetzt gibt es eine Lücke in dieser geordneten Reihenfolge. Nach Mars folgt ein Raum mit einer Berechnung von 4+24=28, in dem noch kein einziger Planet gesehen wurde. Können wir glauben, dass der Gründer des Universums diesen Raum leer gelassen hat? Natürlich nicht. Von hier aus kommen wir zur Jupiterentfernung in Form der Berechnung 4+48=52 und schließlich zur Saturnentfernung - 4+96=100.

Diese beiden Aussagen zu allen spezifischen Typologien und Umlaufradien scheinen aus der Antike zu stammenAstronomie. Viele dieser Theorien stammen aus der Zeit vor dem 17. Jahrhundert.
Einfluss
Titius war ein Schüler des deutschen Philosophen Christian Freiherr von Wolff (1679-1754). Der zweite Teil des eingefügten Textes in Bonnets Werk basiert auf von Wolffs Werk von 1723, Vernünftige Gedanken von den Wirkungen der Natur.
Die Literatur des 20. Jahrhunderts schreibt die Urheberschaft der Titius-Bode-Regel einem deutschen Philosophen zu. Wenn dem so war, konnte Titius von ihm lernen. Eine weitere ältere Referenz wurde von James Gregory im Jahr 1702 in seinen Astronomiae Physicae et geometryae Elementa geschrieben, wo die Folge der Planetenentfernungen 4, 7, 10, 16, 52 und 100 eine geometrische Folge des Verhältnisses 2 wurde.
Dies ist Newtons nächste Formel und wurde auch in den Schriften von Benjamin Martin und Thomas Ceard gefunden, Jahre bevor Bonnets Buch in Deutschland veröffentlicht wurde.
Weitere Arbeiten und praktische Implikationen
Titius und Bode hofften, dass das Gesetz zur Entdeckung neuer Planeten führen würde, und tatsächlich trug die Entdeckung von Uranus und Ceres, deren Entfernung gut mit dem Gesetz übereinstimmt, zu seiner Akzeptanz in der wissenschaftlichen Welt bei.
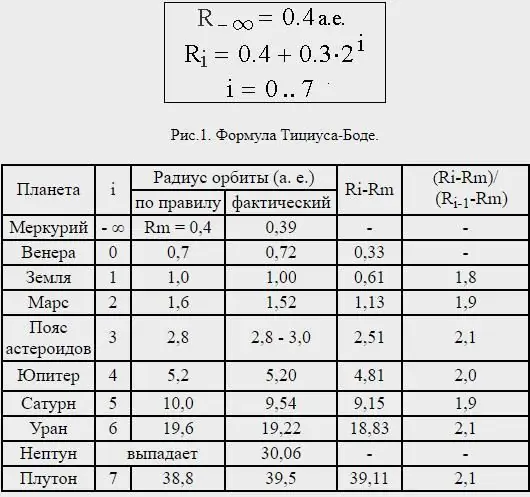
Allerdings war die Entfernung von Neptun sehr inkonsistent, und tatsächlich befindet sich Pluto - jetzt nicht als Planet betrachtet - in einer durchschnittlichen Entfernung, die ungefähr dem Titius-Bode-Gesetz entspricht, das für den nächsten Planeten außerhalb von Uranus vorhergesagt wird.
Das ursprünglich veröffentlichte Gesetz wurde von allen bekannten Planeten - Merkur und Saturn - mit einer Lücke dazwischen ungefähr erfülltvierten und fünften Planeten. Diese g alt bis zur Entdeckung des Uranus im Jahr 1781 als interessante, aber nicht sehr wichtige Figur, die in die Reihe passt.
Basierend auf dieser Entdeckung rief Bode zur Suche nach einem fünften Planeten auf. Ceres, das größte Objekt im Asteroidengürtel, wurde 1801 an Bodes vorhergesagter Position gefunden. Das Gesetz von Bode wurde weithin akzeptiert, bis Neptun 1846 entdeckt wurde und sich als unvereinbar mit dem Gesetz herausstellte.
Zur gleichen Zeit strich eine große Anzahl von Asteroiden, die im Gürtel entdeckt wurden, Ceres von der Liste der Planeten. Das Bodesche Gesetz wurde 1898 vom Astronomen und Logiker Charles Sanders Peirce als Beispiel für Denkfehler diskutiert.

Entwicklung des Problems
Die Entdeckung von Pluto im Jahr 1930 verkomplizierte das Problem weiter. Auch wenn es nicht mit der vom Bodeschen Gesetz vorhergesagten Position übereinstimmte, war es ungefähr die Position, die das Gesetz für Neptun vorhersagte. Die anschließende Entdeckung des Kuipergürtels und insbesondere des Objekts Eris, das massereicher als Pluto ist, aber nicht dem Bodeschen Gesetz entspricht, diskreditierte die Formel weiter.
Serdas Beitrag
Der Jesuit Thomas Cerda hielt 1760 den berühmten Astronomiekurs in Barcelona am Königlichen Lehrstuhl für Mathematik des Kollegiums von Sant Jaume de Cordelle (Königliches und königliches Seminar der Adligen von Cordell). In Cerdas' Tratado erscheinen Planetenentfernungen, die durch Anwendung von Keplers drittem Gesetz erh alten werden, mit einer Genauigkeit von 10-3.
Wenn wir als 10 die Entfernung von der Erde nehmen undAufrunden auf Ganzzahl, geometrische Progression [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, von n=2 bis n=8, kann ausgedrückt werden. Und unter Verwendung einer kreisförmigen, gleichmäßigen, fiktiven Bewegung zur Kepler-Anomalie können die Rn-Werte, die den Verhältnissen jedes Planeten entsprechen, als rn=(Rn - R1) / (Rn-1 - R1) erh alten werden, was 1,82 ergibt; 1, 84; 1, 86; 1,88 und 1,90, wobei rn=2 - 0,02 (12 - n) eine explizite Beziehung zwischen der Keplerschen Kontinuität und dem Titius-Bode-Gesetz ist, die als zufällige numerische Koinzidenz angesehen wird. Das Ergebnis der Berechnung liegt nahe bei zwei, aber die Zwei kann durchaus als Rundung der Zahl 1, 82 betrachtet werden.

Die Durchschnittsgeschwindigkeit des Planeten von n=1 bis n=8 verringert die Entfernung von der Sonne und unterscheidet sich von der gleichmäßigen Abnahme bei n=2, um sich von n=7 zu erholen (Orbitalresonanz). Dies beeinflusst die Entfernung von der Sonne zum Jupiter. Aber auch der Abstand zwischen allen anderen Objekten im Rahmen der berüchtigten Regel, der der Artikel gewidmet ist, wird durch diese mathematische Dynamik bestimmt.
Theoretischer Aspekt
Es gibt keine solide theoretische Erklärung für die Titius-Bode-Regel, aber es ist möglich, dass jedes stabile Planetensystem angesichts der Kombination aus Bahnresonanz und fehlenden Freiheitsgraden eine hohe Wahrscheinlichkeit hat, das in beschriebene Modell zu wiederholen diese Theorie der beiden Wissenschaftler.
Da dies ein mathematischer Zufall und kein "Naturgesetz" sein kann, wird es manchmal eher als Regel denn als "Gesetz" bezeichnet. Der Astrophysiker Alan Boss argumentiert jedoch, dass dies einfach istZufall, und die planetarische Wissenschaftszeitschrift Icarus akzeptiert keine Artikel mehr, die versuchen, verbesserte Versionen des „Gesetzes“bereitzustellen.
Orbitalresonanz
Orbitalresonanz von großen umlaufenden Körpern erzeugt Regionen um die Sonne, die keine langfristig stabilen Umlaufbahnen haben. Die Ergebnisse der Planetenentstehungssimulation unterstützen die Idee, dass ein zufällig ausgewähltes stabiles Planetensystem wahrscheinlich die Titius-Bode-Regel erfüllt.

Dubrulle und Graner
Dubrulle und Graner zeigten, dass Potenzgesetz-Abstandsregeln eine Folge von Modellen kollabierender Wolken von Planetensystemen sein können, die zwei Symmetrien aufweisen: Rotationsinvarianz (die Wolke und ihr Inh alt sind achsensymmetrisch) und Skaleninvarianz (die Wolke und sein Inh alt sieht in allen Maßstäben gleich aus).
Letzteres ist ein Merkmal vieler Phänomene, von denen angenommen wird, dass sie eine Rolle bei der Planetenentstehung spielen, wie zum Beispiel Turbulenzen. Die von Titius und Bode vorgeschlagene Entfernung von der Sonne zu den Planeten des Sonnensystems wurde im Rahmen der Studien von Dubrulle und Graner nicht revidiert.






