Beim Peer-Review beispielsweise, um die Wettbewerbsfähigkeit von Produkten zu bewerten, ist wie bei jeder wissenschaftlichen Arbeit eine statistische Datenverarbeitung notwendig. Letztere beginnt mit der Bestimmung der Konsistenz von Expertenmeinungen, deren numerischer Ausdruck der Konkordanzkoeffizient ist.
Warum brauchen wir eine Expertenkonsensbewertung?
Diese Einschätzung ist zum einen notwendig, weil die Meinungen der Experten zu den geschätzten Parametern sehr unterschiedlich sein können. Die Bewertung erfolgt zunächst, indem die Indikatoren in eine Rangfolge gebracht und ihnen ein bestimmter Signifikanzkoeffizient (Gewicht) zugeordnet wird. Ein inkonsistentes Ranking führt dazu, dass diese Koeffizienten statistisch unzuverlässig sind. Die Gutachten von Sachverständigen mit ihrer erforderlichen Anzahl (mehr als 7-10) sollten gemäß dem normalen Gesetz verteilt werden.
Das Konzept des Konkordanzkoeffizienten
Also. Konsistenz ist Übereinstimmung. Der Koeffizient ist eine dimensionslose Größe, die das Verhältnis der Streuung zur maximalen Streuung im allgemeinen Fall angibt. Lassen Sie uns diese Konzepte verallgemeinern.
Konkordanzkoeffizient ist eine Zahl von 0 bis 1, die die Konsistenz von Expertenmeinungen anzeigt, wennRanking einiger Eigenschaften. Je näher dieser Wert an 0 liegt, desto geringer wird die Konsistenz betrachtet. Wenn der Wert dieses Koeffizienten weniger als 0,3 beträgt, gelten die Meinungen von Experten als widersprüchlich. Wenn der Wert des Koeffizienten im Bereich von 0,3 bis 0,7 liegt, wird die Konsistenz als durchschnittlich betrachtet. Ein Wert über 0,7 gilt als hohe Konsistenz.
Anwendungsfälle
Bei der Durchführung statistischer Untersuchungen können Situationen auftreten, in denen ein Objekt nicht durch zwei Sequenzen charakterisiert werden kann, die statistisch mit dem Konkordanzkoeffizienten verarbeitet werden, sondern durch mehrere Sequenzen, die von Experten entsprechend mit dem gleichen Niveau von bewertet werden Professionalität in einem bestimmten Bereich.
Die Konsistenz des von Experten durchgeführten Rankings muss ermittelt werden, um die Richtigkeit der Hypothese zu bestätigen, dass Experten relativ genaue Messungen vornehmen, was die Bildung verschiedener Gruppierungen in Expertengruppen ermöglicht, die maßgeblich von menschlichen Faktoren bestimmt werden, vor allem wie unterschiedliche Ansichten, Konzepte, unterschiedliche wissenschaftliche Schulen, die Art der beruflichen Tätigkeit usw.
Kurze Beschreibung der Rangmethode. Seine Vor- und Nachteile
Beim Ranking wird die Rangmethode verwendet. Sein Wesen liegt darin, dass jeder Eigenschaft des Objekts ein eigener spezifischer Rang zugeordnet wird. Außerdem wird jedem in der Expertengruppe enth altenen Experten dieser Rang zugeteiltunabhängig, was zur Notwendigkeit führt, diese Daten zu verarbeiten, um die Konsistenz von Expertenmeinungen zu ermitteln. Dieser Prozess wird durch die Berechnung des Konkordanzkoeffizienten durchgeführt.
Der Hauptvorteil der Rangmethode ist ihre einfache Implementierung.
Die Hauptnachteile der Methode sind:
- eine kleine Anzahl von Ranking-Objekten, da es schwierig wird, objektive Ranking-Werte zuzuweisen, wenn ihre Anzahl 15-20 übersteigt;
- Aufgrund der Verwendung dieser Methode bleibt die Frage offen, wie weit die untersuchten Objekte in ihrer Aussagekraft voneinander entfernt sind.
Bei der Anwendung dieser Methode muss berücksichtigt werden, dass die Bewertungen auf einer Art probabilistischem Modell beruhen und daher angesichts des Umfangs mit Vorsicht anzuwenden sind.
Konkordanzrangkoeffizient nach Kendall
Wird verwendet, um die Beziehung zwischen quantitativen und qualitativen Merkmalen zu bestimmen, die homogene Objekte charakterisieren, und wird nach demselben Prinzip geordnet.
Dieser Koeffizient wird durch die Formel bestimmt:
t=2S/(n(n-1)), wobei
S - die Summe der Differenzen zwischen der Anzahl der Sequenzen und der Anzahl der Inversionen beim zweiten Merkmal;
n - Anzahl der Beobachtungen.

Rechenalgorithmus:
- Die x-Werte sind in aufsteigender oder absteigender Reihenfolge angeordnet.
- Die y-Werte sind in der Reihenfolge angeordnet, in der sie den x-Werten entsprechen.
- Bestimmen Sie für jeden aufeinanderfolgenden Rang von y, wie viele höhere Rangwerte darauf folgen. Sie werden addiert und das Übereinstimmungsmaß von Rangfolgen in x und y berechnet.
- In ähnlicher Weise wird die Anzahl der Ränge von y mit niedrigeren Werten berechnet, die sich ebenfalls addieren.
- Addiere die Anzahl der Ränge mit höheren Werten und die Anzahl der Ränge mit niedrigeren Werten, was den Wert S ergibt.
Dieser Koeffizient zeigt die Beziehung zwischen zwei Variablen und wird in den meisten Fällen als Kendall-Rangkorrelationskoeffizient bezeichnet. Eine solche Abhängigkeit kann grafisch dargestellt werden.
Bestimmung des Koeffizienten
Wie wird es gemacht? Wenn die Anzahl der bewerteten Merkmale oder Faktoren 2 übersteigt, wird der Konkordanzkoeffizient verwendet, der im Wesentlichen eine multiple Variante der Rangkorrelation ist.
Sei vorsichtig. Die Berechnung des Konkordanzkoeffizienten basiert auf dem Verhältnis der Abweichung der Summe der Rangquadrate von der durchschnittlichen Summe der Rangquadrate, multipliziert mit 12, zum Quadrat der Experten, multipliziert mit der Differenz zwischen der dritten Potenz der Zahl der Objekte und die Anzahl der Objekte.
Rechenalgorithmus
Um zu verstehen, woher die Zahl 12 im Zähler der Rechenformel kommt, schauen wir uns den Bestimmungsalgorithmus an.
Für jede Zeile mit den Rängen eines bestimmten Experten wird die Summe der Ränge berechnet, die ein Zufallswert ist.
Der Konkordanzkoeffizient ist allgemein definiert als das Verhältnis der Varianzschätzung (D) zum Maximalwert der Varianzschätzung(Dmax). Formulieren wir nacheinander die Definitionen dieser Größen.
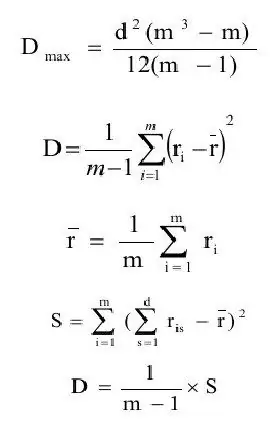
where ravg - Erwartungsschätzung;
m - Anzahl der Objekte.
Durch Einsetzen der resultierenden Formeln in Bezug auf D durch Dmax erh alten wir die endgültige Formel für den Konkordanzkoeffizienten:
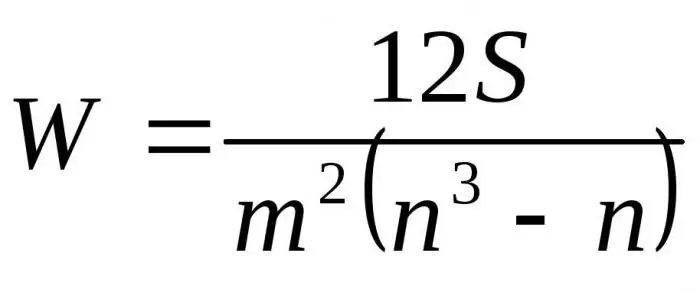
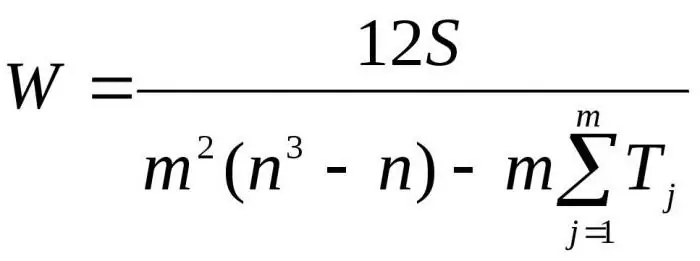
Hier ist m die Anzahl der Experten, n die Anzahl der Objekte.
Die erste Formel wird verwendet, um den Konkordanzfaktor zu bestimmen, wenn es keine verwandten Ränge gibt. Die zweite Formel wird verwendet, wenn es verwandte Ränge gibt.
Also ist die Berechnung des Konkordanzkoeffizienten beendet. Was weiter? Der erh altene Wert wird anhand des Pearson-Koeffizienten auf Signifikanz bewertet, indem dieser Koeffizient mit der Anzahl der Experten und mit der Anzahl der Freiheitsgrade (m-1) multipliziert wird. Das resultierende Kriterium wird mit dem Tabellenwert verglichen, und wenn der Wert des ersten den letzten übersteigt, spricht man von der Signifikanz des untersuchten Koeffizienten.
Bei verwandten Rängen wird die Berechnung des Pearson-Kriteriums etwas komplizierter und erfolgt nach folgendem Verhältnis: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Beispiel
Nehmen Sie an, dass die Expertenmethode die Wettbewerbsfähigkeit von Butter bewertet, die in einem Einzelhandelsnetz verkauft wird. Lassen Sie uns ein Beispiel für die Berechnung des Konkordanzkoeffizienten geben. Vor der Bewertung der Wettbewerbsfähigkeit ist eine Verbrauchereinstufung erforderlichEigenschaften dieses Produkts, die in die Bewertung einfließen. Nehmen wir an, dass diese Eigenschaften folgende sind: Geschmack und Geruch, Konsistenz und Aussehen, Farbe, Verpackung und Etikettierung, Fettgeh alt, Handelsname, Hersteller, Preis.
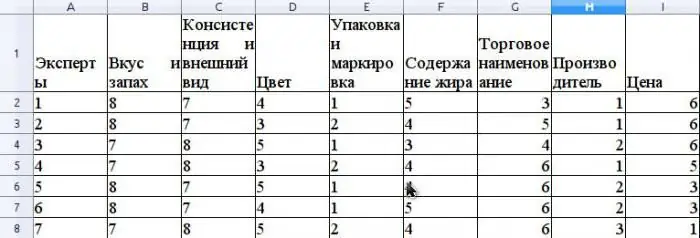
Gehen Sie davon aus, dass die Expertengruppe aus 7 Experten besteht. Die Abbildung zeigt die Ergebnisse der Rangfolge dieser Eigenschaften.
Der Durchschnittswert von r wird als arithmetisches Mittel berechnet und beträgt 31,5. Um S zu finden, summieren Sie die quadrierten Differenzen zwischen ris und r Durchschnitt gemäß der Formel oben, und bestimmen Sie, dass der Wert von S 1718 ist.
Berechnen Sie den Konkordanzkoeffizienten mit der Formel, ohne verwandte Ränge zu verwenden (Ränge wären verwandt, wenn der gleiche Expert Advisor die gleichen Ränge für verschiedene Eigenschaften hätte).
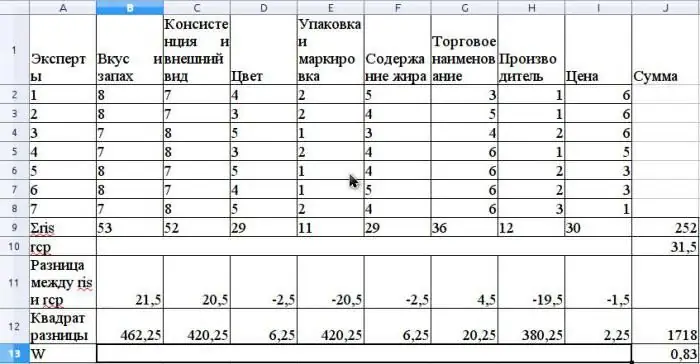
Der Wert dieses Koeffizienten beträgt 0,83. Dies weist auf einen starken Konsens unter Experten hin.
Überprüfen Sie die Signifikanz mit dem Pearson-Test:
7 x 0,83 x (8-1)=40,7.
Der tabellarische Test nach Pearson beträgt bei einem Signifikanzniveau von 1 % 18,5 und bei 5 % - 14,1..
Das Beispiel demonstriert die Einfachheit und Zugänglichkeit der Berechnung für jeden, der die Grundlagen mathematischer Berechnungen kennt. Um sie zu lindern,Verwenden Sie Tabellenkalkulationsformulare.
Zum Schluss
Der Konkordanzkoeffizient zeigt also die Konsistenz der Meinungen mehrerer Experten. Je weiter er von 0 entfernt und näher an 1 liegt, desto konsistenter sind die Meinungen. Diese Koeffizienten müssen durch Berechnung des Pearson-Kriteriums bestätigt werden.






