In der Mathematik ist die Summation (gekennzeichnet durch das große griechische Sigma-Symbol) eine Menge von Summanden von Zahlen. Was ist der Betrag? Dies ist das Ergebnis einer solchen Aktion. Addiert man die Zahlen nacheinander von links nach rechts, so ist das Zwischenergebnis eine Teilsumme.
Wie hoch ist der Betrag?
Die zu summierenden Zahlen können ganzzahlig, rational, reell oder komplex sein. Darüber hinaus können andere Arten von Werten hinzugefügt werden: Vektoren, Matrizen, Polynome und im Allgemeinen Elemente einer beliebigen additiven Gruppe (oder sogar eines Monoids).
Wenn die Anzahl der Elemente der Terme endlich ist, dann ergibt die Summation immer einen wohldefinierten Wert. Die Summierung einer unendlichen Folge von Werten wird als Reihe bezeichnet. Sein Wert kann oft anhand eines Limits bestimmt werden (obwohl der Wert manchmal unendlich sein kann).
Sequenzen
Die Summe der Zahlen [3, 7, 2, 1] kann durch einen Ausdruck definiert werden, dessen Wert die Summe der darin enth altenen Ziffern ist, zum Beispiel 3 + 7 + 2 + 1=13. Da die Zusatzassoziativ hängt die Summe nicht von der Gruppierung der Terme ab, z. B. (3 + 7) + (2 + 1) und 3 + ((7 + 2) + 1) sind beide gleich neun, daher wird normalerweise auf Klammern verzichtet. Die Addition ist auch kommutativ, sodass das Umordnen der Terme den Wert der Summe nicht ändert. Beachten Sie, dass diese Eigenschaft bei unendlicher Summierung möglicherweise nicht funktioniert.

Es gibt keine spezielle Notation für das Summieren von Folgen dieser Art. Bei weniger als zwei Elementen gibt es nur eine leichte Nuance. Die Summierung einer Folge eines Gliedes enthält kein Pluszeichen (es ist von der Form der Zahl selbst nicht zu unterscheiden), und wenn es überhaupt keine Elemente gibt, kann es nicht einmal geschrieben werden (sondern kann mit bezeichnet werden seinen Wert "0"). Wenn jedoch die Terme der Folge durch ein bestimmtes Muster, beispielsweise eine Funktion, spezifiziert werden, kann der Summationsoperator nützlich oder sogar unerlässlich sein.
Aufnahme
Um zu verstehen, was eine Summe ist, muss man auch ihr Aussehen analysieren.
Um eine Folge von ganzen Zahlen von 1 bis 100 zu summieren, wird oft ein Ausdruck verwendet, der Auslassungspunkte enthält, um die fehlenden Elemente anzuzeigen: 1 + 2 + 3 + 4 + … + 99 + 100. Das Muster ist ziemlich einfach in diesem Beispiel zu sehen. Für komplexere Optionen ist es jedoch erforderlich, die zum Ermitteln des Werts der Elemente verwendete Regel genau anzugeben, was mit dem Summationsoperator "Σ" erreicht werden kann. Mit diesem Symbol (Sigma) können Sie die folgende Notation anwenden:
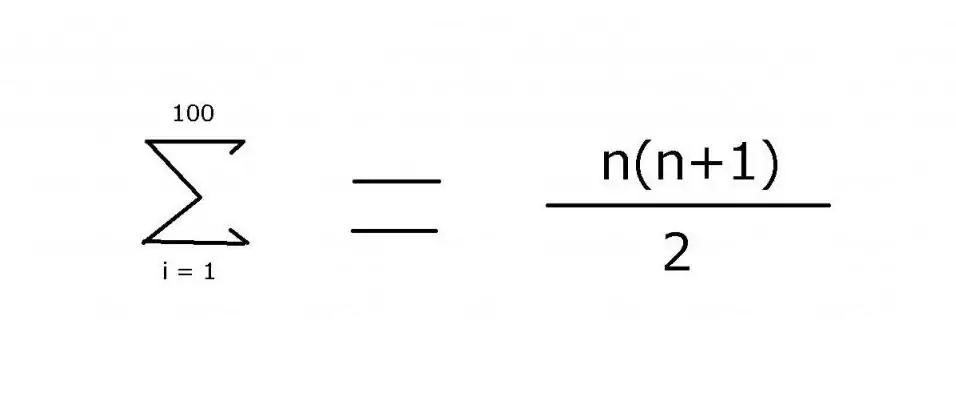
Der Wert dieses Ausdrucks ist 5050. Er kann durch mathematische Induktion gefunden werden, woraus der zweite Teil der Formel stammt.
Für verschiedene Sequenzen ändert sich die Formel. Der Aufzeichnungsprozess reduziert sich darauf, das Urbild einer unendlichen Folge zu suchen und es dann mit einer Formel zu beschreiben. Danach ist es nicht schwer zu verstehen, wie hoch der Betrag in einem bestimmten Fall ist.
Wenn klargestellt werden soll, dass Zahlen mit Vorzeichen (Plus oder Minus) addiert werden, spricht man von algebraischer Summe. In der Theorie elektrischer Sch altungen berücksichtigen die Sch altungsgesetze von Kirchhoff beispielsweise die algebraische Summe von Strömen in einem Netzwerk von Leitern, die sich an einem Punkt treffen, und geben Strömen, die in einen Knoten hinein und aus ihm heraus fließen, entgegengesetzte Vorzeichen.






