Eine lineare Funktion ist eine gerade Linie, die entlang einer Fläche gezogen wird. Es kann in verschiedene Typen und Modelle unterteilt werden. Im Folgenden betrachten wir die Formeln, um es zu erh alten, sowie um seine Perfektion in der Ebene zu erreichen. In den Zeichnungen können Sie dies vollständig überprüfen und verstehen, wie es aussehen sollte.
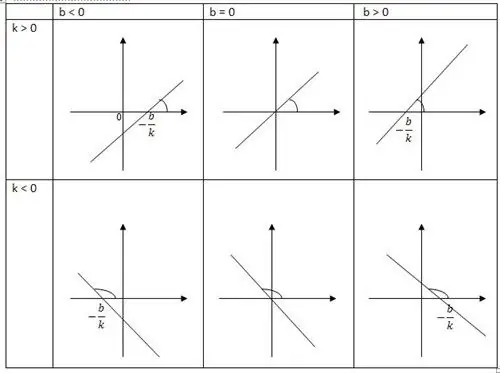
Lineare Funktion y=kx + b
Dieser Wert ist ein genaues Maß für eine Variable in einer Ansicht. Inkrement bezieht sich auf die grundlegende Eigenschaft einer linearen Funktion, sie wird proportional zum inkrementierten Argument. Mit anderen Worten stellt die Funktion eine Verallgemeinerung der direkten Proportionalität dar. Eine Gerade ist ein Graph einer linearen Funktion. Hierher kommt sein Name. Eine reelle Variable berührt eine andere reelle Funktion.
Eigenschaften
Lineare Funktion ist eine Erzeugende einer Geraden, die eine positive Richtung der x-Achse hat. Einer seiner bestimmenden Steigungsfaktoren ist k, er bestimmt den Tangens des Winkels a. Die in positiver Richtung der x-Achse gebildete Gerade ist k. Die andere Koordinate b gibt anPunktkoordinaten sowie den Schnittpunkt der Geraden mit der Achse.
Was sind nichtlineare Funktionen?
Funktionen, die nicht linear sind, nennt man nichtlinear. Dies ist eine mathematische Beziehung zwischen Variablen. Nichtlineare können nicht als y=ax + b ausgedrückt werden. Dieser Begriff wird in jenen Momenten verwendet, in denen es notwendig ist, den allgemeinen Fall zu studieren. Dieser Prozess beginnt mit den niedrigeren Graden. In diesem Fall werden quadratische Korrekturen berücksichtigt. Eine solche Funktion hat stetige Krümmung.
Die betrachtete nichtlineare Gleichung ist willkürlich. Ein Beispiel für eine nichtlineare Funktion ist y=x2. Häufig werden die Begriffe „lineare Funktion“verwendet, mit einer Verfeinerung und dem Zusatz „homogen“. Es kann auf eine exakte lineare Abbildung von X angewendet werden, das ein Vektorraum ist. Eine lineare Funktion ist das ganze System.






