Eine der Hauptaufgaben der Analyse dynamischer Regelsysteme ist die Lösung des Problems ihrer Stabilität. Ihre Stabilität ist eines der wichtigsten Merkmale des Managementkonzepts. Das System gilt als instabil, wenn es nicht in seine ursprüngliche Position zurückkehrt, sondern nach einigen Änderungen am Eingang weiterschwingt oder unter dem Einfluss einer unerwünschten Störung steht.
Definition des Hauptbegriffs
Nach dem Konzept der Systemstabilität ist der Zustand seines Gleichgewichts darauf zurückzuführen, dass keine Störfaktoren darauf einwirken. Die Differenz zwischen Soll- und Ist-Zustand geht in dieser Situation gegen Null. Stabilität ist seine Fähigkeit, in seinen ursprünglichen Gleichgewichtszustand zurückzukehren, nachdem die Störung, die zu seiner Verletzung geführt hat, beendet ist. Ein instabiles System entfernt sich aufgrund des Einflusses einer Störung vom Gleichgewichtszustand oder oszilliert, dessen Amplitude allmählich erfolgtsteigend.

Stabilitätsbedingungen
Für die Stabilität eines Systems mit konstanter Zeit müssen die folgenden beiden Bedingungen erfüllt sein:
- Sie erstellt eine begrenzte Ausgabe für jede Eingabe; Wenn es keine Eingabe gibt, muss die Ausgabe unabhängig von Anfangsbedingungen Null sein.
- Die Stabilität des Systems kann als absolute oder relative Stabilität bezeichnet werden. Der vorgestellte Begriff wird im Zusammenhang mit einer Studie verwendet, in der bestimmte Größen mit ihren Betriebsbedingungen verglichen werden. Stabilität ist das Endergebnis, das durch das Ergebnis entsteht.
Wenn die Ausgabe eines Systems unendlich ist, selbst wenn eine endliche Eingabe darauf angewendet wird, dann wird es als instabil bezeichnet, d.h. inhärent stabil, es hat eine begrenzte Beendigung, wenn ein begrenzter Start angewendet wird selbst.
In diesem Fall wird der Input als verschiedene Angriffspunkte des Einflusses der äußeren Umgebung auf das System verstanden. Der Output ist das Endprodukt seiner Aktivität, das in Form der transformierten Eingabedaten vorliegt.
In einem kontinuierlichen linearen Zeitsystem kann die Stabilitätsbedingung für eine bestimmte Impulsantwort geschrieben werden.
Wenn es diskret ist, kann der Stabilitätsindex auch für eine bestimmte Impulsantwort geschrieben werden.
Für einen instabilen Zustand sowohl in kontinuierlichen als auch in beschränkten Systemen sind diese Ausdrücke unendlich.
Arten von Stabilität und Störungen
Unter StatikDie Stabilität des Systems wird als seine Fähigkeit verstanden, die Wiederherstellung des ursprünglichen (oder nahe am ursprünglichen) Regimes nach einer kleinen Störung sicherzustellen. Unter dem in diesem Zusammenhang vorgestellten Konzept betrachten sie eine Schwankung, die ihr Verh alten beeinflusst, unabhängig davon, wo der Anstieg oder Abfall auftritt und wie groß er ist. Auf dieser Grundlage erlauben uns diese Modi, die dem ursprünglichen nahe kommen, ihn als linear zu betrachten.
Dynamische Stabilität von Systemen ist die Fähigkeit letzterer, nach einer großen Störung den Ausgangszustand wiederherzustellen.
Unter einer großen Fluktuation versteht man eine solche Bewegung, deren Einfluss und ihr entsprechendes Verh alten die Zeit ihres Bestehens, die Größe und den Ort ihres Auftretens bestimmen.
Aufgrund dessen wird das System in diesem Bereich als nichtlinear definiert.
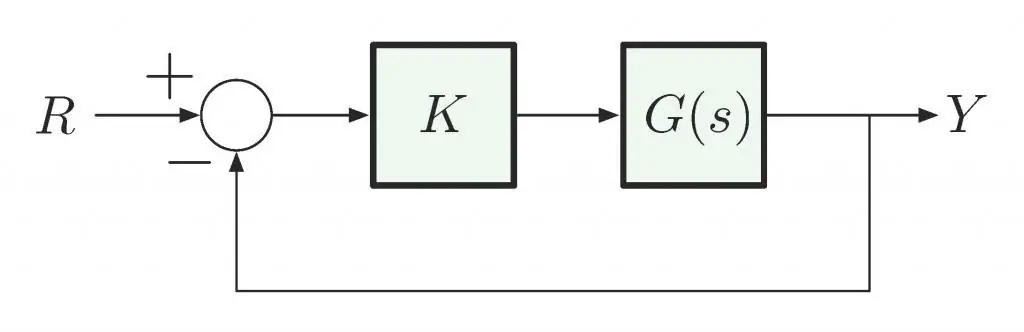
Kriterien zur Bestimmung der Nachh altigkeit
Die Hauptbedingung für die Stabilität eines linearen Systems ist nicht die Art der Störung, sondern ihre Struktur. Es wird angenommen, dass diese Stabilität "im Kleinen" bestimmt wird, wenn ihre Grenzen nicht festgelegt sind. Die Stabilität "im Großen" wird durch die Grenzen und die Übereinstimmung der tatsächlichen Abweichungen mit diesen festgelegten Grenzen bestimmt.
Zur Bestimmung der Stabilität des Systems werden folgende Kriterien herangezogen:
- Wurzelkriterium;
- Stodola-Kriterium;
- Hurwitz-Kriterium;
- Nyquist-Kriterium;
- Mikhailov-Kriterium und andere
Das Root-Kriterium und die Bewertungstechnik von Stodola werden verwendet, um die Stabilität einzelner Links zu bestimmenund offene Systeme. Das Hurwitz-Kriterium ist algebraisch und erlaubt es, die Stabilität geschlossener Systeme ohne Verzögerung zu bestimmen. Die Nyquist- und Mikhailov-Kriterien sind Häufigkeitskriterien. Sie werden verwendet, um die Stabilität geschlossener Systeme anhand ihres Frequenzgangs zu bestimmen.

Wurzelkriterium
Erlaubt es Ihnen, die Stabilität des Systems anhand der Form der Übertragungsfunktion zu bestimmen. Seine Verh altenseigenschaften werden durch ein charakteristisches Polynom (den Nenner der Übertragungsfunktion) beschrieben. Wenn wir den Nenner gleich Null setzen, erlauben uns die Wurzeln der resultierenden Gleichung, den Grad der Stabilität zu bestimmen.
Nach diesem Kriterium ist das lineare System stabil, wenn alle Nullstellen der Gleichung in der linken Halbebene liegen. Wenn mindestens einer von ihnen an der Stabilitätsgrenze liegt, ist er auch am Limit. Befindet sich mindestens einer von ihnen in der rechten Halbebene, kann das System als instabil betrachtet werden.
Stodola-Kriterium
Er folgt aus der Wurzeldefinition. Nach dem Stodola-Kriterium kann ein lineares System als stabil angesehen werden, wenn alle Koeffizienten des Polynoms positiv sind.
Hurwitz-Kriterium
Dieses Kriterium wird für das charakteristische Polynom eines abgeschlossenen Systems verwendet. Gemäß dieser Technik ist eine ausreichende Bedingung für die Stabilität die Tatsache, dass der Wert der Determinante und aller Hauptdiagonalen der Matrix größer als Null ist. Wenn mindestens einer von ihnen gleich istNull, es wird auf der Stabilitätsgrenze betrachtet. Wenn es mindestens eine negative Determinante gibt, sollte sie als instabil betrachtet werden.
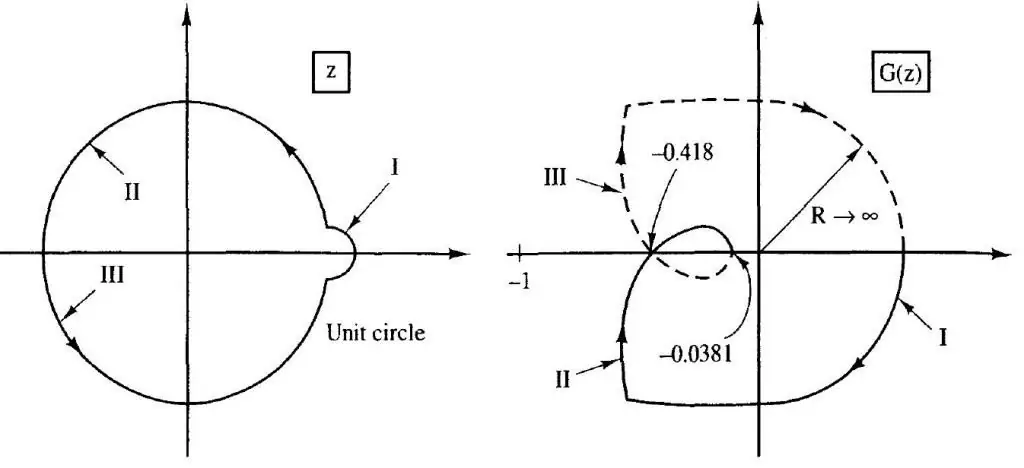
Nyquist-Kriterium
Die Grundlage dieser Technik ist die Konstruktion einer Kurve, die die Enden eines Vektors einer Variablen verbindet, die die Übertragungsfunktion darstellt. Die Formulierung des Kriteriums lautet wie folgt: Ein geschlossenes System gilt als stabil, wenn die Funktionskurve keinen Punkt mit den Koordinaten (-1, j0) auf der komplexen Ebene einschließt.
Finanzielles Soliditätssystem
Finanzielle Belastbarkeit ist der Zustand, in dem das System, d. h. die wichtigsten Märkte und Institutionen, gegenüber wirtschaftlichen Schocks widerstandsfähig und bereit sind, seine Kernfunktionen der Cashflow-Vermittlung, des Risikomanagements und der Zahlungsvereinbarungen reibungslos auszuführen.
Aufgrund des gegenseitigen Abhängigkeitsverhältnisses bei der Bereitstellung von Dolmetschern (sowohl vertikal als auch horizontal) muss die Analyse das gesamte Finanzintermediationssystem umfassen. Mit anderen Worten, neben dem Bankensektor müssen auch Nichtbanken analysiert werden, die in der einen oder anderen Form an der Intermediation beteiligt sind. Dazu gehören zahlreiche Arten von Institutionen, darunter Maklerfirmen, Investmentfonds, Versicherer und andere (verschiedene) Unternehmen. Bei der Analyse eines Systems der Finanzstabilität wird untersucht, inwieweit die gesamte Struktur externen und internen Schocks standh alten kann. Natürlich führen nicht immer Schocks zu Krisen, sondern das instabile Finanzumfeld selbstalleine kann die gesunde Entwicklung der Wirtschaft behindern.
Verschiedene Theorien identifizieren die Ursachen der finanziellen Instabilität. Ihre Relevanz kann je nach Zeitraum und den in den Analyseumfang einbezogenen Ländern variieren. Unter den problematischen Faktoren, die das gesamte Finanzsystem betreffen, werden in der Literatur üblicherweise die folgenden identifiziert:
- rasche Liberalisierung des Finanzsektors;
- unzureichende Wirtschaftspolitik;
- Ungezielter Wechselkursmechanismus;
- ineffiziente Ressourcenallokation;
- schwache Aufsicht;
- Unzureichende Regulierung der Rechnungslegung und Abschlussprüfung.
Mögliche Ursachen treten nicht nur kollektiv, sondern auch einzeln oder in zufälliger Kombination auf, sodass die Analyse der Finanzstabilität eine äußerst schwierige Aufgabe ist. Die Fokussierung auf einzelne Branchen verzerrt das große Ganze, sodass die Fragestellungen im Zuge der Untersuchung der Finanzstabilität in ihrer Komplexität betrachtet werden müssen.

Die Analyse der Stabilität des Unternehmenssystems erfolgt in mehreren Schritten.
Zunächst werden absolute und relative Indikatoren der Finanzstabilität ausgewertet und analysiert. In der zweiten Stufe werden die Faktoren nach ihrer Bedeutung verteilt, ihr Einfluss qualitativ und quantitativ bewertet.
Finanzkraftkennzahlen von Unternehmen
Die Finanzlage des Unternehmens, seine Stabilität hängt weitgehend von der optimalen Struktur der Kapitalquellen ab, dh dem optimalen Verhältnis von Fremdkapital zu Eigenmittelnder Vermögensstruktur der Gesellschaft und in erster Linie vom Verhältnis von Anlage- und Umlaufvermögen sowie der Vermögenslage der Gesellschaft.
Daher ist es wichtig, die Struktur der Risikokapitalquellen zu untersuchen und den Grad der finanziellen Stabilität und des Risikos zu bewerten. Dazu werden die Koeffizienten der Systemstabilität verwendet:
- Autonomiekoeffizient (Unabhängigkeit) - der Kapitalanteil in der Bilanz;
- Abhängigkeitsquote - Anteil des Fremdkapitals an der Bilanz;
- aktuelle Schuldenquote - das Verhältnis der kurzfristigen Finanzverbindlichkeiten zur Bilanz;
- Financial Stability Ratio (langfristige finanzielle Unabhängigkeit) - das Verhältnis von Kapital und langfristigen Schulden zur Bilanz;
- Debt Coverage Ratio (Solvabilitätsquote) - das Verhältnis von Kapital zu Schulden;
- Financial Leverage Ratio (Finanzrisikoverhältnis) - das Verhältnis von Fremdkapital zu Kapital.

Je höher das Niveau von Indikatoren wie Autonomie, finanzielle Stabilität, Deckung des Fremdkapitals, desto niedriger das Niveau einer anderen Gruppe von Koeffizienten (Abhängigkeit, aktuelle Verschuldung, langfristige Verpflichtungen gegenüber Investoren) und dementsprechend die Stabilität der Finanzlage des Unternehmens. Finanzielle Hebelwirkung wird auch als finanzielle Hebelwirkung bezeichnet.






