Elastizitätsmodul ist eine physikalische Größe, die das elastische Verh alten eines Materials charakterisiert, wenn eine äußere Kraft in einer bestimmten Richtung auf es einwirkt. Das elastische Verh alten eines Materials ist seine Verformung im elastischen Bereich.
Geschichte der Untersuchung der Elastizität von Materialien

Die physikalische Theorie elastischer Körper und ihr Verh alten unter Einwirkung äußerer Kräfte wurde von dem englischen Wissenschaftler des 19. Jahrhunderts, Thomas Young, eingehend betrachtet und studiert. Das eigentliche Konzept der Elastizität wurde jedoch bereits 1727 vom Schweizer Mathematiker, Physiker und Philosophen Leonhard Euler entwickelt, und die ersten Experimente zum Elastizitätsmodul wurden 1782 durchgeführt, also 25 Jahre vor der Arbeit von Thomas Jung, des venezianischen Mathematikers und Philosophen Jacopo Ricatti.
Thomas Youngs Verdienst liegt darin, dass er der Elastizitätstheorie ein schlankes modernes Aussehen gab, das anschließend in Form eines einfachen und dann verallgemeinerten Hookeschen Gesetzes formalisiert wurde.
Physikalische Natur der Elastizität
Jeder Körper besteht aus Atomen, zwischen denen Anziehungs- und Abstoßungskräfte wirken. Das Gleichgewicht dieser Kräfte istZustand und Parameter der Materie unter gegebenen Bedingungen. Die Atome eines Festkörpers beginnen sich zu verschieben, wenn unbedeutende äußere Zug- oder Druckkräfte auf sie einwirken, wodurch eine Kraft mit entgegengesetzter Richtung und gleicher Größe entsteht, die dazu neigt, die Atome in ihren ursprünglichen Zustand zurückzubringen.
Bei einer solchen Verschiebung von Atomen steigt die Energie des gesamten Systems. Experimente zeigen, dass bei kleinen Dehnungen die Energie proportional zum Quadrat dieser Dehnungen ist. Das bedeutet, dass die Kraft als Ableitung nach der Energie proportional zur ersten Potenz der Dehnung ausfällt, also linear davon abhängt. Bei der Beantwortung der Frage, was ist der Elastizitätsmodul, können wir sagen, dass dies der Proportionalitätskoeffizient zwischen der auf das Atom wirkenden Kraft und der durch diese Kraft verursachten Verformung ist. Die Dimension des Elastizitätsmoduls ist dieselbe wie die Dimension des Drucks (Pascal).
Elastizitätsgrenze
Der Elastizitätsmodul gibt per Definition an, wie viel Spannung auf einen Festkörper ausgeübt werden muss, damit er sich zu 100% verformt. Alle Feststoffe haben jedoch eine Elastizitätsgrenze von 1 % Dehnung. Dies bedeutet, dass, wenn eine geeignete Kraft ausgeübt wird und der Körper um einen Betrag von weniger als 1 % verformt wird, der Körper nach Beendigung dieser Kraft seine ursprüngliche Form und Abmessungen wieder genau annimmt. Wird eine zu große Kraft aufgebracht, bei der der Verformungswert 1 % übersteigt, stellt der Körper nach Beendigung der äußeren Kraft seine ursprünglichen Abmessungen nicht mehr wieder her. Im letzteren Fall spricht man von der Existenz einer Restverformung, das heißtNachweis, dass die Elastizitätsgrenze des Materials überschritten wurde.
E-Modul in Aktion
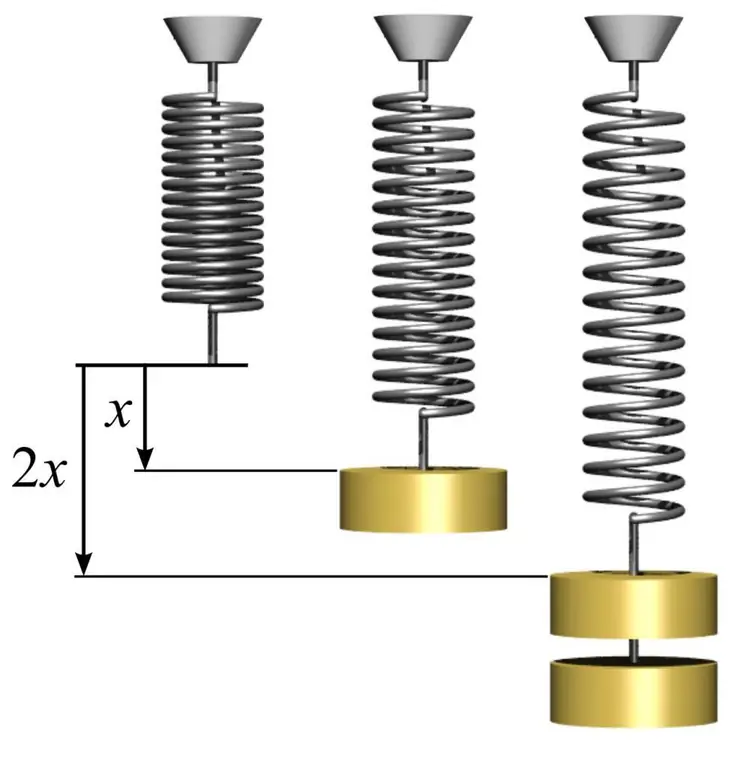
Um den Elastizitätsmodul zu bestimmen und zu verstehen, wie man ihn verwendet, können Sie ein einfaches Beispiel mit einer Feder geben. Dazu müssen Sie eine Metallfeder nehmen und die Fläche des Kreises messen, den ihre Windungen bilden. Dies geschieht mit der einfachen Formel S=πr², wobei n pi gleich 3,14 und r der Radius der Windung der Feder ist.
Messen Sie als nächstes die Länge der Feder l0 ohne Belastung. Wenn Sie eine beliebige Last der Masse m1 an eine Feder hängen, wird diese bis zu einem bestimmten Wert l1 länger. Der Elastizitätsmodul E lässt sich in Kenntnis des Hookeschen Gesetzes nach folgender Formel berechnen: E=m1gl0/(S(l 1-l0)), wobei g die Beschleunigung im freien Fall ist. In diesem Fall stellen wir fest, dass die Verformung der Feder im elastischen Bereich 1 % deutlich überschreiten kann.
Wenn Sie den Elastizitätsmodul kennen, können Sie das Ausmaß der Verformung unter Einwirkung einer bestimmten Spannung vorhersagen. Wenn wir in diesem Fall eine weitere Masse m2 an die Feder hängen, erh alten wir den folgenden Wert der relativen Verformung: d=m2g/ (SE), wobei d - relative Verformung im elastischen Bereich.
Isotropie und Anisotropie
Elastizitätsmodul ist eine Eigenschaft eines Materials, die die Stärke der Bindung zwischen seinen Atomen und Molekülen beschreibt, jedoch kann ein bestimmtes Material mehrere unterschiedliche Elastizitätsmodule haben.
Tatsache ist, dass die Eigenschaften jedes Festkörpers von seiner inneren Struktur abhängen. Sind die Eigenschaften in allen Raumrichtungen gleich, spricht man von einem isotropen Material. Solche Substanzen haben eine homogene Struktur, sodass die Einwirkung einer äußeren Kraft in verschiedenen Richtungen auf sie die gleiche Reaktion des Materials hervorruft. Alle amorphen Materialien sind isotrop, wie Gummi oder Glas.
Anisotropie ist ein Phänomen, das durch die Richtungsabhängigkeit der physikalischen Eigenschaften eines Festkörpers oder einer Flüssigkeit gekennzeichnet ist. Alle Metalle und darauf basierende Legierungen haben das eine oder andere Kristallgitter, dh eine geordnete und keine chaotische Anordnung von Ionenkernen. Bei solchen Materialien variiert der Elastizitätsmodul in Abhängigkeit von der Wirkungsachse der äußeren Belastung. Zum Beispiel haben Metalle mit kubischer Symmetrie wie Aluminium, Kupfer, Silber, Refraktärmetalle und andere drei verschiedene Elastizitätsmodule.
Schubmodul
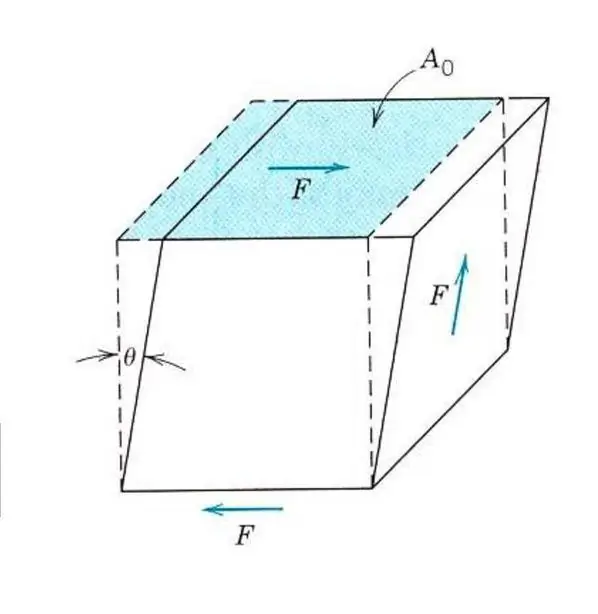
Die Beschreibung der elastischen Eigenschaften selbst eines isotropen Materials erfordert keine Kenntnis des Elastizitätsmoduls. Denn neben Zug und Druck können auch Schubspannungen oder Torsionsbeanspruchungen auf das Material einwirken. In diesem Fall wird es anders auf äußere Kraft reagieren. Um die elastische Scherverformung zu beschreiben, wird ein Analogon des Youngschen Moduls, des Schermoduls oder des Elastizitätsmoduls der zweiten Art eingeführt.
Alle Materialien widerstehen Scherspannungen weniger als Zug oder Druck, daher ist der Schermodulwert für sie 2-3 mal kleiner als der Wert des Elastizitätsmoduls. Somit ist für Titan, dessen Elastizitätsmodul gleich 107 GPa ist, der Schermodul gleichnur 40 GPa, für Stahl sind es 210 GPa bzw. 80 GPa.
Elastizitätsmodul von Holz

Holz ist ein anisotropes Material, weil Holzfasern entlang einer bestimmten Richtung orientiert sind. Entlang der Fasern wird der Elastizitätsmodul von Holz gemessen, da er über die Fasern 1-2 Größenordnungen kleiner ist. Die Kenntnis des Elastizitätsmoduls für Holz ist wichtig und wird bei der Konstruktion von Holzplattenstrukturen berücksichtigt.
Die Werte des Elastizitätsmoduls von Holz für einige Baumarten sind in der folgenden Tabelle aufgeführt.
| Baumansicht | E-Modul in GPa |
| Lorbeerbaum | 14 |
| Eukalyptus | 18 |
| Zeder | 8 |
| Fichte | 11 |
| Kiefer | 10 |
| Eiche | 12 |
Es ist zu beachten, dass die angegebenen Werte für einen bestimmten Baum um bis zu 1 GPa abweichen können, da sein Elastizitätsmodul von der Dichte des Holzes und den Wachstumsbedingungen beeinflusst wird.

Schermoduli für verschiedene Baumarten liegen im Bereich von 1-2 GPa, zum Beispiel für Kiefer sind es 1,21 GPa und für Eiche 1,38 GPa, d.h. Holz hält Schubspannungen praktisch nicht stand. Diese Tatsache muss bei der Herstellung von Holztragwerken berücksichtigt werden, die nur auf Zug oder Druck arbeiten sollen.
Elastische Eigenschaften von Metallen
Im Vergleich zum E-Modul von Holz sind die Durchschnittswerte dieses Werts für Metalle und Legierungen um eine Größenordnung höher, wie in der folgenden Tabelle dargestellt.
| Metall | E-Modul in GPa |
| Bronze | 120 |
| Kupfer | 110 |
| Stahl | 210 |
| Titan | 107 |
| Nickel | 204 |
Die elastischen Eigenschaften von Metallen mit kubischer Syngonie werden durch drei elastische Konstanten beschrieben. Solche Metalle umfassen Kupfer, Nickel, Aluminium, Eisen. Besitzt ein Metall eine hexagonale Syngonie, so werden bereits sechs Konstanten benötigt, um seine elastischen Eigenschaften zu beschreiben.
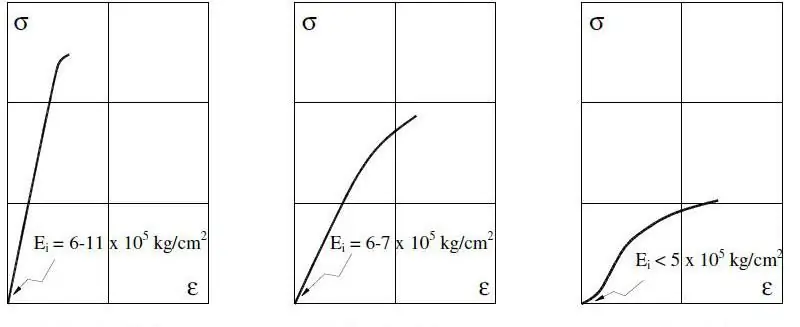
Bei metallischen Systemen wird der Elastizitätsmodul innerhalb von 0,2 % Dehnung gemessen, da bereits im unelastischen Bereich große Werte auftreten können.






