Im Physikstudium in der 10. Klasse wird das Thema Dipole berücksichtigt. Was bedeutet dieses Konzept und mit welchen Formeln wird es berechnet?
Einführung
Wenn Sie einen Dipol in den Raum eines gleichförmigen elektrischen Feldes platzieren, können Sie ihn als Kraftlinien darstellen. Ein Dipol ist ein System, in dem es zwei Ladungen mit identischen Parametern gibt, die jedoch entgegengesetzte Punktladungen sind. Außerdem ist der Abstand zwischen ihnen viel geringer als der Abstand zu irgendeinem Punkt des Dipolfelds. Der Begriff des Dipolmoments wird im Schulkurs Elektrodynamik (10. Klasse) behandelt.
Die Achse des Dipols ist eine Gerade, die durch die Punkte beider Ladungen verläuft. Ein Dipolarm ist ein Vektor, der eine Ladung verbindet und gleichzeitig von negativ geladenen Teilchen zu positiv geladenen Teilchen geht. Ein elektrischer Dipol ist durch das Vorhandensein eines solchen Zustands wie ein Dipol oder ein elektrisches Moment gekennzeichnet.
Per Definition ist ein Dipolmoment ein Vektor, der numerisch gleich dem Produkt aus der Dipolladung und seinem Arm ist. Darüber hinaus ist es mit der Schulter des Dipols gleichgerichtet. Bei Nullgleichheit der Summe der Kräfte berechnen wir den Wert des Moments. Für den Winkel, der zwischen dem Dipolmoment und bestehtRichtwirkung des elektrischen Feldes, das Vorhandensein eines mechanischen Moments ist charakteristisch.
Oft fällt es Menschen schwer, den auf die Dipolstruktur wirkenden Modul zu berechnen. Hier müssen die Besonderheiten bei der Berechnung des Winkels "Alpha" berücksichtigt werden. Es ist bekannt, dass der Dipol von der Gleichgewichtslage abweicht. Aber das Dipolmoment selbst hat einen rückstellenden Charakter, da es eher in Bewegung ist.
Berechnungen
Wenn dieses Dipolmoment in das Medium eines inhomogenen elektrischen Feldes gebracht wird, entsteht zwangsläufig eine Kraft. In einer solchen Umgebung werden die Indikatoren der Summe der Kräfte nicht Null sein. Folglich wirken auf das Dipolmoment Kräfte mit punktuellem Charakter. Die Größe des Dipolarms ist viel kleiner.
Die Formel kann folgendermaßen geschrieben werden: F=q (E2 - E1)=qdE, wobei d die elektrische Felddifferenz ist.
Suche nach den Merkmalen des untersuchten physikalischen Konzepts
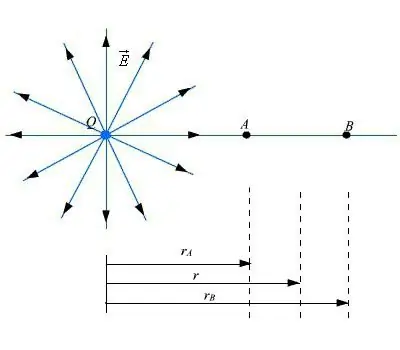
Sehen wir uns das Thema weiter an. Um die Charakteristik des elektrischen Feldes zu bestimmen, wenn es unter Verwendung eines Ladungssystems erzeugt und auf kleinem Raum lokalisiert wird, müssen eine Reihe von Berechnungen durchgeführt werden. Ein Beispiel stellen Atome und Moleküle dar, die in ihrer Zusammensetzung elektrisch geladene Kerne und Elektronen aufweisen.
Wenn es notwendig ist, ein Feld in einer Entfernung zu suchen, die größer ist als die Dimensionen, die den Bereich ausmachen, in dem sich die Partikel befinden, verwenden wir eine Reihe von exakten Formeln, die sehr komplex sind. Es ist möglich, einfacher zu verwendenungefähre Ausdrücke. Nehmen wir an, dass Punktsätze von Ladungen qk an der Erzeugung des elektrischen Feldes beteiligt sind. Sie befinden sich auf kleinem Raum.
Um die Berechnung der Eigenschaften durchzuführen, die das Feld hat, ist es erlaubt, alle Gebühren des Systems zu kombinieren. Ein solches System wird als Punktladung Q betrachtet. Die Größenindikatoren sind die Summe der Ladungen, die im ursprünglichen System vorhanden waren.
Lastplatz
Stellen wir uns vor, dass der Ort der Ladung überall dort angezeigt wird, wo sich das Gebührensystem qk befindet. Wenn Änderungen am Standort vorgenommen werden, ist ein solcher Einfluss, wenn er in einem kleinen Bereich ausgedrückte Grenzen hat, vernachlässigbar, fast nicht wahrnehmbar für das Feld aus der Sicht. Innerhalb solcher Annäherungsgrenzen der Stärke und des Potentials, die das elektrische Feld hat, werden Bestimmungen unter Verwendung herkömmlicher Formeln vorgenommen.
Wenn die Summe der Gesamtladung des Systems Null ist, sehen die Parameter der angezeigten Näherung grob aus. Daraus lässt sich schließen, dass das elektrische Feld einfach fehlt. Wenn es notwendig ist, eine genauere Annäherung zu erh alten, sammeln Sie im Geist separate Gruppen positiver und negativer Ladungen des betrachteten Systems.
Im Falle einer Verschiebung ihrer "Zentren" relativ zu anderen können die Feldparameter in einem solchen System als ein Feld beschrieben werden, das zwei Punktladungen mit gleichem Betrag und entgegengesetztem Vorzeichen hat. Es wird darauf hingewiesen, dass sie in Bezug auf andere verschoben sind. BereitstellenFür eine genauere Charakterisierung des Ladungssystems in Bezug auf die Parameter dieser Näherung wird es notwendig sein, die Eigenschaften eines Dipols in einem elektrischen Feld zu untersuchen.
Begriffseinführung
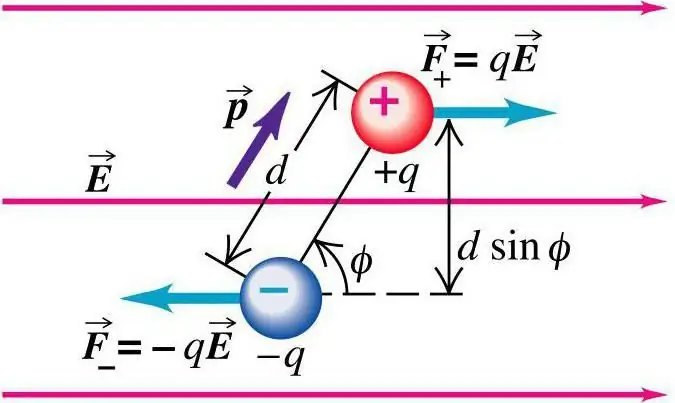
Kehren wir zur Definition zurück. Ein elektrischer Dipol ist die Definition eines Systems mit zwei Punktladungen. Sie haben die gleiche Größe und entgegengesetzte Vorzeichen. Außerdem befinden sich solche Schilder in geringem Abstand zu anderen Schildern.
Sie können die Charakteristik des Prozesses berechnen, der durch einen Dipol erzeugt wird und durch zwei Punktladungen repräsentiert wird: +q und −q, und sie befinden sich in einem relativen Abstand a zu den anderen.

Rechenfolge
Berechnen wir zunächst das Potential und die Intensität, die der Dipol auf seiner axialen Oberfläche hat. Dies ist eine gerade Linie, die zwischen zwei Ladungen verläuft. Unter der Voraussetzung, dass sich der Punkt A in einem Abstand befindet, der gleich r relativ zum zentralen Teil des Dipols ist, und wenn es sich um r >> a handelt, ist dies nach dem Überlagerungsprinzip für das Feldpotential an diesem Punkt sinnvoll Verwenden Sie den Ausdruck, um die Parameter des elektrischen Dipols zu berechnen.
Die Größe des Stärkevektors wird nach dem Superpositionsprinzip berechnet. Zur Berechnung der Feldstärke wird das Konzept des Verhältnisses von Potential und Feldstärke verwendet:
Ex=−Δφ /Δx.
Unter solchen Bedingungen wird die Richtung des Intensitätsvektors längs zur Dipolachse angegeben. Zur Berechnung des Moduls gilt die Standardformel.
WichtigKlarstellungen
Zu beachten ist, dass die Abschwächung des elektrischen Dipolfeldes schneller erfolgt, als es eine Punktladung erfährt. Der Abfall des Dipolfeldpotentials ist umgekehrt proportional zum Quadrat der Entfernung, und die Feldstärke ist umgekehrt proportional zur dritten Potenz der Entfernung.
Mit ähnlichen, aber umständlicheren Methoden werden die Parameter des Potentials und der Feldstärke des Dipols an beliebigen Punkten gefunden, deren Positionsparameter mit einer solchen Berechnungsmethode wie Polarkoordinaten bestimmt werden: die Entfernung zum Mittelpunkt des elektrischen Dipols (r) und Winkel (θ).
Berechnung mit Spannungsvektor
Das Konzept des Intensitätsvektors E wird in zwei Punkte unterteilt:
- Radial (Er), das in Längsrichtung zur Geraden gerichtet ist.
- Eine solche Gerade verbindet den angegebenen Punkt und den Mittelpunkt des Dipols mit der Senkrechten darauf Eθ.
Diese Zerlegung jeder Komponente richtet sich nach dem Verlauf der Veränderung, der bei allen Koordinaten des zu beobachtenden Punktes auftritt. Sie können es anhand des Verhältnisses finden, das Feldstärkeindikatoren zu möglichen Modifikationen in Beziehung setzt.
Um die Vektorkomponente bei der Feldstärke zu finden, ist es wichtig, die Art der Beziehung in den Potentialänderungen festzustellen, die aufgrund der Verschiebung des Beobachtungspunkts in Richtung der Vektoren auftreten.
Berechnen Sie die senkrechte Komponente
Wenn Sie fertig sindBei diesem Verfahren ist es wichtig zu berücksichtigen, dass der Ausdruck für den Betrag bei einer kleinen senkrechten Verschiebung durch Änderung des Winkels bestimmt wird: Δl=rΔθ. Die Betragsparameter für diese Feldkomponente werden gleich sein.
Nachdem man das Verhältnis erh alten hat, ist es möglich, das Feld des elektrischen Dipols an einem beliebigen Punkt zu bestimmen, um ein Bild mit den Kraftlinien dieses Felds zu erstellen.
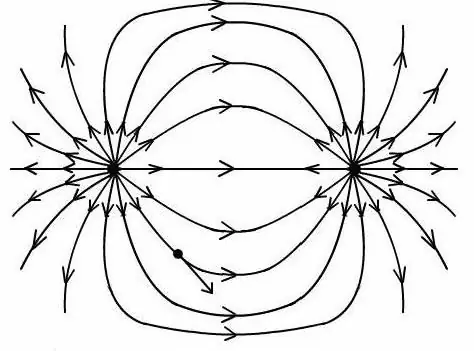
Es ist wichtig zu beachten, dass alle Formeln zur Bestimmung des Potentials und der Feldstärke eines Dipols nur auf dem Produkt der Werte, die eine Dipolladung hat, und dem Abstand zwischen ihnen funktionieren.
Dipolmoment
Der Titel der beschriebenen Arbeit ist eine vollständige Beschreibung der elektrischen Art von Eigenschaften. Es hat den Namen "Dipolmoment des Systems".
Durch Definition eines Dipols, der ein System von Punktladungen ist, kann festgestellt werden, dass er durch das Vorhandensein von Achsensymmetrie gekennzeichnet ist, wenn die Achse eine gerade Linie ist, die durch mehrere Ladungen verläuft.
Um die volle Charakteristik des Dipols einzustellen, geben Sie die Orientierungsrichtung an, die die Achse hat. Zur Vereinfachung der Berechnungen kann der Dipolmomentvektor angegeben werden. Der Wert seiner Größe ist gleich der Größe des Dipolmoments, und der Richtungsvektor unterscheidet sich durch das Zusammenfallen von ihm und der Achse des Dipols. Also ist p=qa, wenn a die Richtung des Vektors ist, der die negativen und positiven Ladungen des Dipols verbindet.
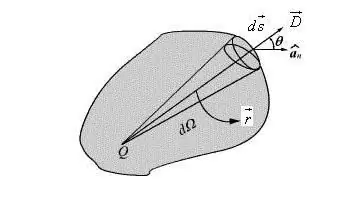
Die Verwendung einer solchen Eigenschaft des Dipols ist bequem und ermöglicht es in den meisten Fällen, die Formel zu vereinfachen und ihr die Form zu gebenVektor. Die Beschreibung des Potentials des Dipolfeldes an einem Punkt beliebiger Richtung wird in Form eines Vektors geschrieben.
Die Einführung von Konzepten wie der Vektorcharakteristik eines Dipols und seines Dipolmoments kann mit einem vereinfachten Modell durchgeführt werden − einer Punktladung in einem einheitlichen Feld, das ein Ladungssystem enthält, dessen geometrische Abmessungen dies tun müssen nicht berücksichtigt werden, aber es ist wichtig, das Dipolmoment zu kennen. Dies ist eine Voraussetzung für die Durchführung von Berechnungen.
Wie sich ein Dipol verhält
Am Beispiel einer solchen Situation ist das Verh alten eines Dipols zu sehen. Die Position zweier Punktladungen hat relativ zueinander einen festen Abstandscharakter. Sie wurden den Bedingungen eines Dipols eines gleichförmigen elektrischen Felds ausgesetzt. Beobachtungen zum Vorgang gemacht. Im Physikunterricht (Elektrodynamik) wird dieser Begriff ausführlich betrachtet. Vom Feld zur Ladung erfolgt die Krafteinwirkung:
F=±qE
Sie sind gleich groß und entgegengesetzt gerichtet. Der Indikator für die Gesamtkraft, die auf den Dipol wirkt, ist Null. Da eine solche Kraft an verschiedenen Stellen wirkt, ist das Gesamtmoment:
M=Fa sin a=qEa sin a=pE sin a
wobei α der Winkel ist, der die Feldstärkevektoren und die Dipolmomentvektoren verbindet. Aufgrund des Vorhandenseins eines Kraftmoments neigt das Dipolmoment des Systems dazu, in die Richtungen des elektrischen Feldstärkevektors zurückzukehren.
Elektrischer Dipol ist ein Konzept, das klar verstanden werden muss. Sie können mehr darüber im Internet lesen. Auch das kannim Physikunterricht in der Schule in der 10. Klasse lernen, wie wir oben besprochen haben.






