Jeder Mensch begegnet im Laufe seines Lebens Körpern, die sich in einem der drei Aggregatzustände der Materie befinden. Der am einfachsten zu untersuchende Aggregatzustand ist Gas. In dem Artikel werden wir das Konzept eines idealen Gases betrachten, die Zustandsgleichung des Systems angeben und auch der Beschreibung der absoluten Temperatur etwas Aufmerksamkeit schenken.
Gaszustand der Materie
Jeder Schüler hat eine ungefähre Vorstellung davon, von welchem Aggregatzustand er spricht, wenn er das Wort "Gas" hört. Dieses Wort wird als Körper verstanden, der in der Lage ist, jedes ihm zur Verfügung gestellte Volumen einzunehmen. Es ist nicht in der Lage, seine Form zu h alten, weil es selbst dem geringsten äußeren Einfluss nicht widerstehen kann. Außerdem behält Gas kein Volumen, was es nicht nur von Feststoffen, sondern auch von Flüssigkeiten unterscheidet.
Ein Gas ist wie eine Flüssigkeit eine flüssige Substanz. Bei der Bewegung fester Körper in Gasen behindern diese diese Bewegung. Die resultierende Kraft wird als Widerstand bezeichnet. Sein Wert hängt davon abGeschwindigkeit des Körpers im Gas.
Starke Beispiele für Gase sind Luft, Erdgas zum Heizen und Kochen, Inertgase (Ne, Ar) zum Füllen von Werbeglühröhren oder zum Schaffen einer inerten (nicht aggressiven, schützenden) Umgebung beim Schweißen.
Ideales Gas
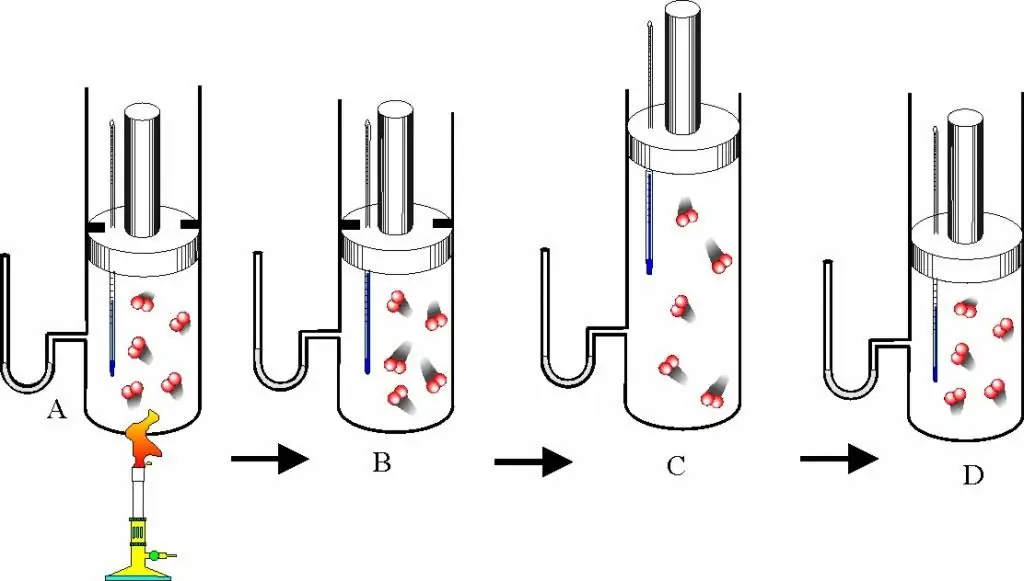
Bevor Sie mit der Beschreibung der Gasgesetze und der Zustandsgleichung fortfahren, sollten Sie die Frage gut verstehen, was ein ideales Gas ist. Dieses Konzept wird in die Molekularkinetiktheorie (MKT) eingeführt. Ein ideales Gas ist jedes Gas, das die folgenden Eigenschaften erfüllt:
- Die Partikel, die es bilden, interagieren nicht miteinander, außer bei direkten mechanischen Kollisionen.
- Infolge der Kollision von Teilchen mit den Gefäßwänden oder untereinander bleiben ihre kinetische Energie und ihr Impuls erh alten, d. h. die Kollision wird als absolut elastisch angesehen.
- Teilchen haben keine Dimensionen, aber eine endliche Masse, d.h. sie ähneln materiellen Punkten.
Es ist natürlich, dass jedes Gas nicht ideal, sondern real ist. Dennoch sind diese Näherungen zur Lösung vieler praktischer Probleme durchaus gültig und können verwendet werden. Es gibt eine allgemeine empirische Regel, die besagt: Unabhängig von der chemischen Natur kann ein Gas, wenn es eine Temperatur über Raumtemperatur und einen Druck in der Größenordnung von Atmosphärendruck oder darunter hat, mit hoher Genauigkeit als ideal angesehen und zur Beschreibung verwendet werden es. Formel der idealen Gaszustandsgleichung.
Clapeyron-Mendelejew-Gesetz
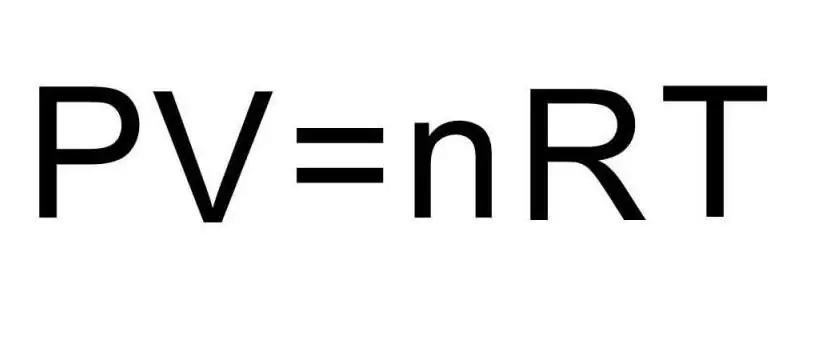
Übergänge zwischen verschiedenen Aggregatzuständen der Materie und Vorgänge innerhalb eines Aggregatzustandes werden von der Thermodynamik behandelt. Druck, Temperatur und Volumen sind drei Größen, die jeden Zustand eines thermodynamischen Systems eindeutig definieren. Die Formel für die Zustandsgleichung eines idealen Gases fasst alle drei Größen zu einer einzigen Gleichung zusammen. Schreiben wir diese Formel:
PV=nRT
Hier P, V, T - jeweils Druck, Volumen, Temperatur. Der Wert von n ist die Stoffmenge in Mol, und das Symbol R bezeichnet die universelle Gaskonstante. Diese Gleichheit zeigt, dass das Produkt aus Stoffmenge und Temperatur umso größer sein muss, je größer das Produkt aus Druck und Volumen ist.

Die Formel für die Zustandsgleichung eines Gases heißt Clapeyron-Mendelejew-Gesetz. 1834 kam der französische Wissenschaftler Emile Clapeyron, der die experimentellen Ergebnisse seiner Vorgänger zusammenfasste, zu dieser Gleichung. Clapeyron verwendete jedoch eine Reihe von Konstanten, die Mendeleev später durch eine ersetzte - die universelle Gaskonstante R (8, 314 J / (molK)). Daher wird diese Gleichung in der modernen Physik nach den Namen französischer und russischer Wissenschaftler benannt.

Andere Gleichungsformen
Oben haben wir die Mendeleev-Clapeyron-Zustandsgleichung für ein ideales Gas im allgemein akzeptierten und geschriebenbequemes Formular. Bei Problemen in der Thermodynamik kann jedoch oft eine etwas andere Form erforderlich sein. Unten stehen drei weitere Formeln, die direkt aus der geschriebenen Gleichung folgen:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Diese drei Gleichungen sind auch für ein ideales Gas universell, nur dass in ihnen Größen wie Masse m, Molmasse M, Dichte ρ und die Anzahl der Teilchen N auftauchen, aus denen das System besteht. Das Symbol kB bezeichnet hier die Boltzmann-Konstante (1, 3810-23J/K).
Boyle-Mariotte-Gesetz
Als Clapeyron seine Gleichung aufstellte, basierte er auf Gasgesetzen, die einige Jahrzehnte zuvor experimentell entdeckt worden waren. Eines davon ist das Boyle-Mariotte-Gesetz. Es spiegelt einen isothermen Prozess in einem geschlossenen System wider, wodurch sich makroskopische Parameter wie Druck und Volumen ändern. Setzen wir T und n konstant in die Zustandsgleichung für ein ideales Gas ein, dann nimmt das Gasgesetz die Form an:
P1V1=P2V 2
Dies ist das Boyle-Mariotte-Gesetz, das besagt, dass das Produkt aus Druck und Volumen während eines beliebigen isothermen Prozesses erh alten bleibt. In diesem Fall ändern sich die Werte P und V selbst.
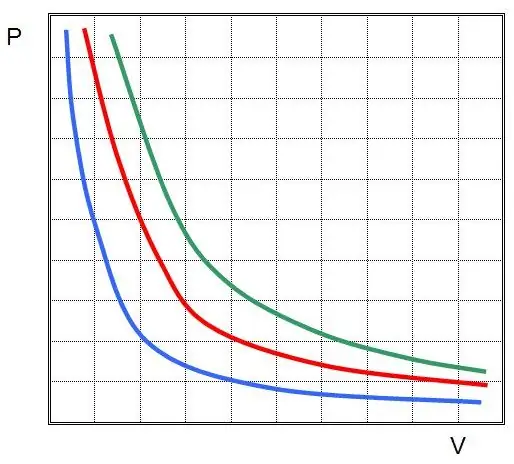
Wenn Sie P(V) oder V(P) zeichnen, dann sind die Isothermen Hyperbeln.
Die Gesetze von Charles und Gay-Lussac
Diese Gesetze beschreiben mathematisch isobar und isochorischProzesse, also solche Übergänge zwischen den Zuständen des Gassystems, bei denen Druck bzw. Volumen erh alten bleiben. Das Gesetz von Charles kann mathematisch wie folgt geschrieben werden:
V/T=const wenn n, P=const.
Das Gesetz von Gay-Lussac wird wie folgt geschrieben:
P/T=const wenn n, V=const.
Wenn beide Gleichungen in Form eines Diagramms dargestellt werden, erh alten wir gerade Linien, die in einem bestimmten Winkel zur x-Achse geneigt sind. Diese Art von Diagramm zeigt eine direkte Proportionalität zwischen Volumen und Temperatur bei konstantem Druck und zwischen Druck und Temperatur bei konstantem Volumen.
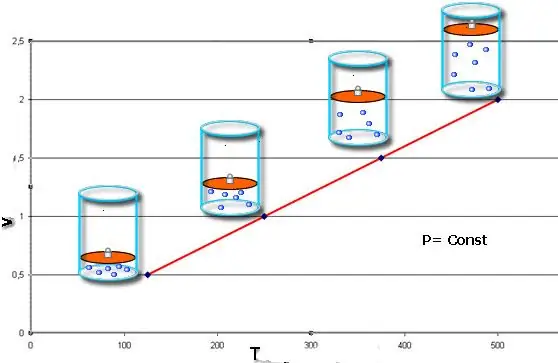
Beachten Sie, dass alle drei betrachteten Gasgesetze die chemische Zusammensetzung des Gases sowie die Änderung seiner Stoffmenge nicht berücksichtigen.
Absolute Temperatur
Im Alltag sind wir es gewohnt, die Celsius-Temperaturskala zu verwenden, da sie bequem ist, um die Prozesse um uns herum zu beschreiben. Wasser kocht also bei 100 oC und gefriert bei 0 oC. In der Physik erweist sich diese Skala als unpraktisch, daher verwendet man die sogenannte absolute Temperaturskala, die Mitte des 19. Jahrhunderts von Lord Kelvin eingeführt wurde. Entsprechend dieser Skala wird die Temperatur in Kelvin (K) gemessen.
Es wird angenommen, dass es bei einer Temperatur von -273, 15 oC keine thermischen Schwingungen von Atomen und Molekülen gibt, ihre Vorwärtsbewegung stoppt vollständig. Diese Temperatur in Grad Celsius entspricht dem absoluten Nullpunkt in Kelvin (0 K). Aus dieser Definitiondie physikalische Bedeutung der absoluten Temperatur folgt: Sie ist ein Maß für die kinetische Energie der Teilchen, aus denen Materie besteht, beispielsweise Atome oder Moleküle.
Neben der obigen physikalischen Bedeutung der absoluten Temperatur gibt es noch andere Ansätze, diese Größe zu verstehen. Eines davon ist das erwähnte Gasgesetz von Charles. Schreiben wir es in der folgenden Form:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Die letzte Gleichheit besagt, dass bei einer bestimmten Stoffmenge im System (z. B. 1 mol) und einem bestimmten Druck (z. B. 1 Pa) das Gasvolumen eindeutig die absolute Temperatur bestimmt. Mit anderen Worten, eine Zunahme des Gasvolumens ist unter diesen Bedingungen nur aufgrund einer Temperaturerhöhung möglich, und eine Volumenabnahme zeigt eine Abnahme des Wertes von T an.
Denken Sie daran, dass im Gegensatz zur Celsius-Temperatur die absolute Temperatur nicht negativ sein kann.
Avogadro-Prinzip und Gasmischungen
Zusätzlich zu den obigen Gasgesetzen führt die Zustandsgleichung für ein ideales Gas auch zu dem Anfang des 19. Jahrhunderts von Amedeo Avogadro entdeckten Prinzip, das seinen Nachnamen trägt. Dieses Prinzip besagt, dass das Volumen eines beliebigen Gases bei konstantem Druck und konstanter Temperatur durch die Stoffmenge im System bestimmt wird. Die entsprechende Formel sieht so aus:
n/V=const wenn P, T=const.
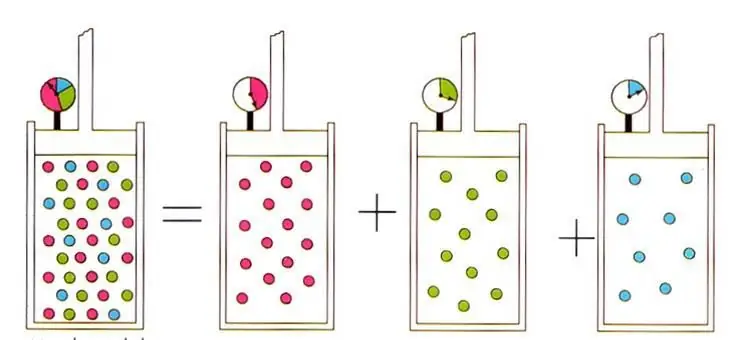
Der geschriebene Ausdruck führt auf das in der idealen Gasphysik bekannte D altonsche Gesetz für Gasgemische. DasDas Gesetz besagt, dass der Partialdruck eines Gases in einem Gemisch eindeutig durch seinen Atombruch bestimmt wird.
Beispiel zur Problemlösung
In einem geschlossenen Gefäß mit starren Wänden, das ein ideales Gas enthält, stieg der Druck infolge der Erwärmung um das Dreifache. Es ist notwendig, die Endtemperatur des Systems zu bestimmen, wenn ihr Anfangswert 25 oC.
war.
Rechnen wir zuerst die Temperatur von Grad Celsius in Kelvin um, wir haben:
T=25 + 273, 15=298, 15 K.
Da die Wände des Gefäßes starr sind, kann der Erwärmungsprozess als isochor angesehen werden. Für diesen Fall wenden wir das Gay-Lussac-Gesetz an, wir haben:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Die Endtemperatur ergibt sich also aus dem Produkt des Druckverhältnisses und der Anfangstemperatur. Durch Gleichsetzen der Daten erh alten wir die Antwort: T2=894,45 K. Diese Temperatur entspricht 621,3 oC.






