Die Kenntnis physikalischer Definitionen ist ein Schlüsselfaktor für die erfolgreiche Lösung verschiedener physikalischer Probleme. In dem Artikel werden wir betrachten, was unter isobaren, isochoren, isothermen und adiabatischen Prozessen für ein ideales Gassystem zu verstehen ist.
Ideales Gas und seine Gleichung
Bevor wir mit der Beschreibung von isobaren, isochoren und isothermen Prozessen fortfahren, wollen wir uns überlegen, was ein ideales Gas ist. Unter dieser Definition in der Physik betrachten sie ein System, das aus einer großen Anzahl von dimensionslosen und nicht wechselwirkenden Teilchen besteht, die sich mit hoher Geschwindigkeit in alle Richtungen bewegen. Tatsächlich handelt es sich um einen gasförmigen Aggregatzustand der Materie, bei dem die Abstände zwischen Atomen und Molekülen deren Größe bei weitem übersteigen und bei dem die potentielle Wechselwirkungsenergie der Teilchen wegen ihrer Kleinheit gegenüber der kinetischen Energie vernachlässigt wird.
Der Zustand eines idealen Gases ist die Gesamtheit seiner thermodynamischen Parameter. Die wichtigsten sind Temperatur, Volumen und Druck. Lassen Sie uns sie mit den Buchstaben T, V bzw. P bezeichnen. In den 30er Jahren des 19. JahrhundertsClapeyron (ein französischer Wissenschaftler) schrieb zuerst eine Gleichung auf, die die angegebenen thermodynamischen Parameter innerhalb einer einzigen Gleichung kombiniert. Es sieht so aus:
PV=nRT,
wobei n und R die Stoffmenge bzw. die Gaskonstante sind.
Was sind Isoprozesse in Gasen?
Wie viele bemerkt haben, verwenden isobare, isochore und isotherme Prozesse das gleiche "iso"-Präfix in ihren Namen. Es bedeutet die Gleichheit eines thermodynamischen Parameters während des gesamten Prozesses, während sich die übrigen Parameter ändern. Beispielsweise zeigt ein isothermer Prozess an, dass dadurch die absolute Temperatur des Systems konstant geh alten wird, während ein isochorer Prozess ein konstantes Volumen anzeigt.
Isoprozesse sind bequem zu untersuchen, da die Festlegung eines der thermodynamischen Parameter zu einer Vereinfachung der allgemeinen Gaszustandsgleichung führt. Es ist wichtig anzumerken, dass die Gasgesetze für alle diese Isoprozesse experimentell entdeckt wurden. Ihre Analyse ermöglichte es Clapeyron, die reduzierte universelle Gleichung zu erh alten.
Isobare, isochore und isotherme Prozesse
Das erste Gesetz wurde für einen isothermen Prozess in einem idealen Gas entdeckt. Heute heißt es Boyle-Mariotte-Gesetz. Da sich T nicht ändert, impliziert die Zustandsgleichung die Gleichheit:
PV=const.
Mit anderen Worten, jede Druckänderung im System führt zu einer umgekehrt proportionalen Volumenänderung, wenn die Temperatur des Gases konstant geh alten wird. Der Graph der Funktion P(V) istÜbertreibung.
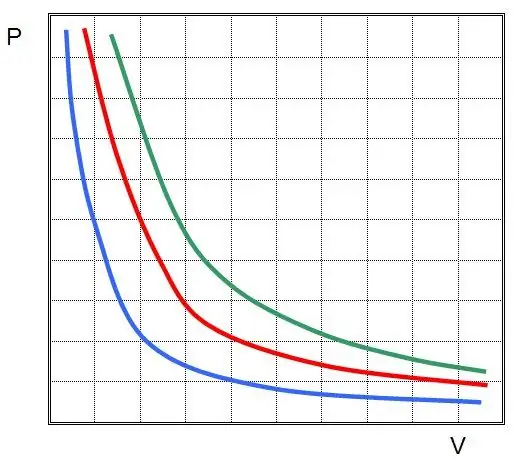
Isobarer Prozess - Dies ist eine Zustandsänderung des Systems, bei der der Druck konstant bleibt. Nachdem wir den Wert von P in der Clapeyron-Gleichung festgelegt haben, erh alten wir das folgende Gesetz:
V/T=konst.
Diese Gleichheit trägt den Namen des französischen Physikers Jacques Charles, der sie Ende des 18. Jahrhunderts erhielt. Die Isobare (grafische Darstellung der V(T)-Funktion) sieht aus wie eine gerade Linie. Je mehr Druck im System ist, desto schneller steigt diese Linie.
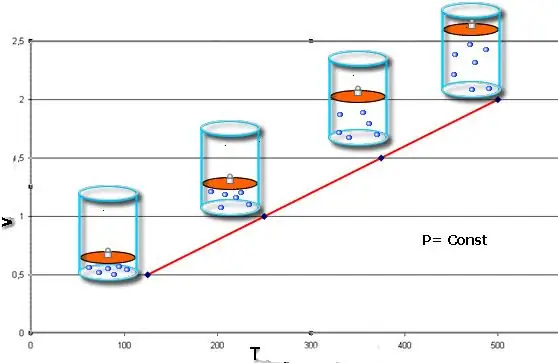
Der isobare Prozess ist einfach umzusetzen, wenn das Gas unter dem Kolben erhitzt wird. Die Moleküle der letzteren erhöhen ihre Geschwindigkeit (kinetische Energie), erzeugen einen höheren Druck auf den Kolben, was zur Expansion des Gases führt und einen konstanten Wert von P aufrechterhält.
Schließlich ist der dritte Isoprozess isochor. Es läuft mit konstanter Lautstärke. Aus der Zustandsgleichung erh alten wir die entsprechende Gleichheit:
P/T=const.
Es ist unter Physikern als Gesetz von Gay-Lussac bekannt. Die direkte Proportionalität zwischen Druck und absoluter Temperatur zeigt, dass der Graph des isochoren Prozesses, wie der Graph der Isobaren, eine Gerade mit positiver Steigung ist.
Es ist wichtig zu verstehen, dass alle Isoprozesse in geschlossenen Systemen ablaufen, d. h. der Wert von n bleibt während ihres Verlaufs erh alten.
Adiabatischer Prozess
Dieser Prozess gehört nicht zur Kategorie "Iso", da sich alle drei thermodynamischen Parameter während seines Durchlaufs ändern. adiabatbezeichnet den Übergang zwischen zwei Zuständen des Systems, in denen es keine Wärme mit der Umgebung austauscht. Somit erfolgt die Expansion des Systems aufgrund seiner internen Energiereserven, was zu einem erheblichen Abfall des Drucks und der absoluten Temperatur darin führt.
Der adiabatische Prozess für ein ideales Gas wird durch die Poisson-Gleichungen beschrieben. Eine davon ist unten dargestellt:
PVγ=const,
wobei γ das Verhältnis der Wärmekapazitäten bei konstantem Druck und konstantem Volumen ist.
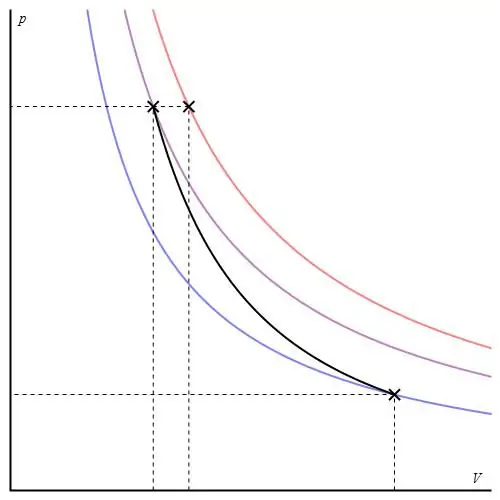
Der adiabatische Graph unterscheidet sich vom isochoren Prozessgraphen und vom isobaren Graphen, ähnelt aber einer Hyperbel (Isotherme). Der Adiabat in den P-V-Achsen verhält sich schärfer als die Isotherme.






