Ideales Gas, die Zustandsgleichung des idealen Gases, seine Temperatur und sein Druck, sein Volumen… die Liste der im entsprechenden Abschnitt der Physik verwendeten Parameter und Definitionen lässt sich noch lange fortführen. Heute werden wir nur über dieses Thema sprechen.
Was wird in der Molekularphysik betrachtet?

Das in diesem Abschnitt betrachtete Hauptobjekt ist ein ideales Gas. Die ideale Gaszustandsgleichung wurde unter Berücksichtigung normaler Umgebungsbedingungen erh alten, und wir werden etwas später darauf eingehen. Nun nähern wir uns diesem "Problem" aus der Ferne.
Nehmen wir an, wir haben eine Menge Gas. Sein Zustand kann anhand von drei Parametern thermodynamischer Natur bestimmt werden. Dies sind natürlich Druck, Volumen und Temperatur. Die Zustandsgleichung des Systems ist in diesem Fall die Formel für die Beziehung zwischen den entsprechenden Parametern. Das sieht so aus: F (p, V, T)=0.
Hier nähern wir uns zum ersten Mal langsam der Entstehung eines solchen IdealsGas. Es wird ein Gas genannt, in dem die Wechselwirkungen zwischen Molekülen vernachlässigbar sind. In der Natur gibt es das im Allgemeinen nicht. Jedoch ist jedes stark verdünnte Gas nahe dran. Stickstoff, Sauerstoff und Luft, die unter normalen Bedingungen vorliegen, weichen kaum vom Ideal ab. Um die Zustandsgleichung für ein ideales Gas zu schreiben, können wir das vereinheitlichte Gasgesetz verwenden. Wir erh alten: pV/T=const.
Verwandtes Konzept Nr. 1: Avogadros Gesetz
Er kann uns sagen, dass, wenn wir die gleiche Anzahl von Molen von absolut beliebigen Gasen nehmen und sie unter die gleichen Bedingungen bringen, einschließlich Temperatur und Druck, dann werden die Gase das gleiche Volumen einnehmen. Insbesondere wurde der Versuch unter Normalbedingungen durchgeführt. Das bedeutet, dass die Temperatur 273,15 Kelvin betrug, der Druck eine Atmosphäre (760 Millimeter Quecksilbersäule oder 101325 Pascal). Mit diesen Parametern nahm das Gas ein Volumen von 22,4 Litern ein. Daher können wir sagen, dass für ein Mol eines beliebigen Gases das Verhältnis der numerischen Parameter ein konstanter Wert ist. Aus diesem Grund wurde beschlossen, diese Zahl mit dem Buchstaben R zu bezeichnen und sie als universelle Gaskonstante zu bezeichnen. Es entspricht also 8,31 Die Einheit ist J/molK.
Ideales Gas. Die ideale Gaszustandsgleichung und ihre Manipulation
Versuchen wir, die Formel umzuschreiben. Dazu schreiben wir es in dieser Form: pV=RT. Als nächstes führen wir eine einfache Aktion aus, multiplizieren beide Seiten der Gleichung mit einer beliebigen Anzahl von Molen. Wir erh alten pVu=uRT. Berücksichtigen wir die Tatsache, dass das Produkt aus Molvolumen unddie Menge der Materie ist einfach das Volumen. Aber schließlich ist die Molzahl gleichzeitig gleich dem Quotienten aus Masse und Molmasse. Genau so sieht die Mendeleev-Clapeyron-Gleichung aus. Es gibt eine klare Vorstellung davon, was für ein System ein ideales Gas bildet. Die Zustandsgleichung für ein ideales Gas hat die Form: pV=mRT/M.
Formel für Druck herleiten
Lassen Sie uns weitere Manipulationen mit den erh altenen Ausdrücken vornehmen. Dazu wird die rechte Seite der Mendeleev-Clapeyron-Gleichung multipliziert und durch die Avogadro-Zahl dividiert. Nun schauen wir uns das Produkt aus Stoffmenge und Avogadro-Zahl genau an. Das ist nichts anderes als die Gesamtzahl der Moleküle im Gas. Aber gleichzeitig ist das Verhältnis der universellen Gaskonstante zur Avogadro-Zahl gleich der Boltzmann-Konstante. Daher können Formeln für den Druck wie folgt geschrieben werden: p=NkT/V oder p=nkT. Hier ist das Symbol n die Partikelkonzentration.
Ideale Gasprozesse
In der Molekularphysik gibt es so etwas wie Isoprozesse. Dies sind thermodynamische Prozesse, die im System bei einem der konstanten Parameter ablaufen. Dabei muss auch die Masse des Stoffes konstant bleiben. Betrachten wir sie genauer. Also die Gesetze eines idealen Gases.
Druck bleibt konstant
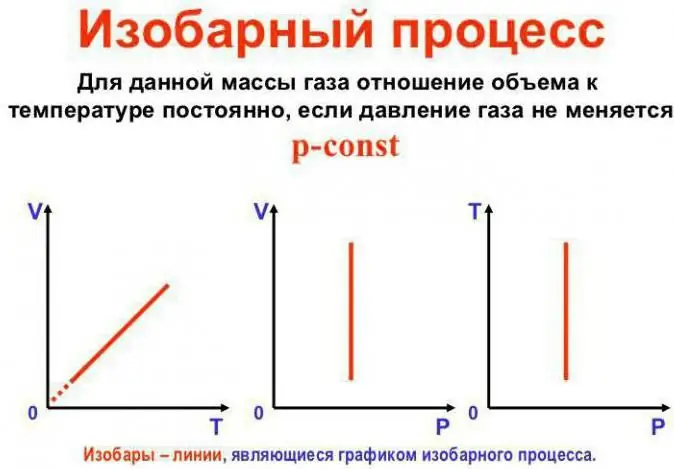
Das ist das Gesetz von Gay-Lussac. Das sieht so aus: V/T=const. Es kann auch anders geschrieben werden: V=Vo (1 + at). Hier ist a gleich 1/273,15 K^-1 und wird als "Volumenausdehnungskoeffizient" bezeichnet. Wir können die Temperatur sowohl in Celsius als auch ersetzendie Kelvin-Skala. Im letzteren Fall erh alten wir die Formel V=Voat.
Lautstärke bleibt konstant

Dies ist das zweite Gesetz von Gay-Lussac, besser bekannt als das Gesetz von Charles. Das sieht so aus: p/T=const. Es gibt noch eine andere Formulierung: p=po (1 + at). Transformationen können gemäß dem vorherigen Beispiel durchgeführt werden. Wie Sie sehen können, sind die idealen Gasgesetze manchmal ziemlich ähnlich.
Temperatur bleibt konstant

Wenn die Temperatur eines idealen Gases konstant bleibt, können wir das Gesetz von Boyle-Mariotte erh alten. Es kann so geschrieben werden: pV=const.
Verwandtes Konzept 2: Partialdruck
Nehmen wir an, wir haben ein Gefäß mit Gasen. Es wird eine Mischung sein. Das System befindet sich im thermischen Gleichgewicht, die Gase selbst reagieren nicht miteinander. Hier bezeichnet N die Gesamtzahl der Moleküle. N1, N2 usw. sind jeweils die Anzahl der Moleküle in jeder der Komponenten der Mischung. Nehmen wir die Druckformel p=nkT=NkT/V. Es kann für einen bestimmten Fall geöffnet werden. Für eine Zweikomponentenmischung hat die Formel die Form: p=(N1 + N2) kT/V. Aber dann stellt sich heraus, dass der Gesamtdruck aus den Partialdrücken jeder Mischung aufsummiert wird. Es sieht also aus wie p1 + p2 und so weiter. Dies sind die Partialdrücke.
Wofür ist es?
Die Formel, die wir erh alten haben, zeigt an, dass der Druck im System von jeder Gruppe von Molekülen stammt. Es kommt übrigens nicht darauf anAndere. Dies machte sich D alton bei der Formulierung des später nach ihm benannten Gesetzes zunutze: In einem Gemisch, in dem Gase nicht chemisch miteinander reagieren, ist der Gesamtdruck gleich der Summe der Partialdrücke.






