Ein wichtiges Teilgebiet der Thermodynamik ist die Untersuchung von Umwandlungen zwischen verschiedenen Phasen eines Stoffes, da diese Prozesse in der Praxis ablaufen und von grundlegender Bedeutung sind, um das Verh alten eines Systems unter bestimmten Bedingungen vorherzusagen. Diese Umwandlungen nennt man Phasenübergänge, denen der Artikel gewidmet ist.
Das Konzept einer Phase und einer Systemkomponente

Bevor wir mit der Betrachtung von Phasenübergängen in der Physik fortfahren, ist es notwendig, das Konzept der Phase selbst zu definieren. Wie aus dem Studium der allgemeinen Physik bekannt ist, gibt es drei Aggregatzustände: gasförmig, fest und flüssig. In einem speziellen Teil der Wissenschaft - in der Thermodynamik - werden die Gesetze für die Phasen der Materie formuliert, nicht für ihre Aggregatzustände. Unter einer Phase versteht man ein bestimmtes Materievolumen, das eine homogene Struktur hat, durch bestimmte physikalische und chemische Eigenschaften gekennzeichnet ist und durch Grenzen, die als Interphase bezeichnet werden, von der übrigen Materie getrennt ist.
Daher enthält das Konzept der "Phase" viel mehr praktisch bedeutsame Informationen über die Eigenschaftenwichtiger als sein Aggregatzustand. Beispielsweise kann der Festkörper eines Metalls wie Eisen in den folgenden Phasen vorliegen: kubisch kubisch (BCC) bei niedriger Temperatur, kubisch zentriert bei niedriger Temperatur (BCC), kubisch flächenzentriert (fcc) bei niedriger Temperatur und kubisch flächenzentriert (fcc). Temperatur nicht magnetisch bcc.
Neben dem Begriff "Phase" verwenden die Gesetze der Thermodynamik auch den Begriff "Komponenten", womit die Anzahl der chemischen Elemente gemeint ist, aus denen ein bestimmtes System besteht. Das bedeutet, dass die Phase entweder einkomponentig (1 chemisches Element) oder mehrkomponentig (mehrere chemische Elemente) sein kann.
Der Satz von Gibbs und das Gleichgewicht zwischen den Phasen des Systems

Um Phasenübergänge zu verstehen, ist es notwendig, die Gleichgewichtsbedingungen zwischen ihnen zu kennen. Diese Bedingungen können mathematisch ermittelt werden, indem das System der Gibbs-Gleichungen für jede von ihnen gelöst wird, wobei angenommen wird, dass der Gleichgewichtszustand erreicht ist, wenn sich die gesamte Gibbs-Energie des von äußeren Einflüssen isolierten Systems nicht mehr ändert.
Als Ergebnis der Lösung des angegebenen Gleichungssystems werden Bedingungen für das Bestehen eines Gleichgewichts zwischen mehreren Phasen erh alten: Ein isoliertes System wird sich erst dann nicht mehr entwickeln, wenn die Drücke, chemischen Potentiale jeder Komponente und Temperaturen in allen Phasen übereinstimmen sind einander gleich.
Gibbs-Phasenregel für das Gleichgewicht

Ein System bestehend aus mehreren Phasen und Komponenten kann nicht nur im Gleichgewicht seinunter bestimmten Bedingungen, beispielsweise bei einer bestimmten Temperatur und einem bestimmten Druck. Einige der Variablen im Gibbs-Theorem für das Gleichgewicht können geändert werden, während sowohl die Anzahl der Phasen als auch die Anzahl der Komponenten, die sich in diesem Gleichgewicht befinden, beibeh alten werden. Die Anzahl der Variablen, die verändert werden können, ohne das Gleichgewicht im System zu stören, nennt man die Anzahl der Freiheiten dieses Systems.
Die Anzahl der Freiheiten l eines aus f Phasen und k Komponenten bestehenden Systems ist eindeutig aus der Gibbs-Phasenregel bestimmt. Diese Regel wird mathematisch wie folgt geschrieben: l + f=k + 2. Wie arbeitet man mit dieser Regel? Sehr einfach. Beispielsweise ist bekannt, dass das System aus f=3 Gleichgewichtsphasen besteht. Was ist die Mindestanzahl von Komponenten, die ein solches System enth alten kann? Sie können die Frage folgendermaßen beantworten: Im Falle eines Gleichgewichts liegen die strengsten Bedingungen vor, wenn es nur bei bestimmten Indikatoren realisiert wird, dh eine Änderung eines thermodynamischen Parameters führt zu einem Ungleichgewicht. Damit ist die Anzahl der Freiheiten l=0. Durch Ersetzen der bekannten Werte von l und f erh alten wir k=1, dh ein System, in dem drei Phasen im Gleichgewicht sind, kann aus einer Komponente bestehen. Ein Paradebeispiel ist der Tripelpunkt von Wasser, wo Eis, flüssiges Wasser und Dampf bei bestimmten Temperaturen und Drücken im Gleichgewicht existieren.
Klassifizierung von Phasenumwandlungen
Wenn Sie beginnen, einige thermodynamische Parameter in einem System im Gleichgewicht zu ändern, können Sie beobachten, wie eine Phase verschwindet und eine andere erscheint. Ein einfaches Beispiel für diesen Vorgang ist das Schmelzen von Eis, wenn es erhitzt wird.
Da die Gibbs-Gleichung nur von zwei Variablen (Druck und Temperatur) abhängt und der Phasenübergang eine Änderung dieser Variablen beinh altet, kann der Übergang zwischen den Phasen mathematisch durch Differenzieren der Gibbs-Energie in Bezug auf seine beschrieben werden Variablen. Diesen Ansatz verfolgte 1933 der österreichische Physiker Paul Ehrenfest, als er eine Klassifikation aller bekannten thermodynamischen Prozesse zusammenstellte, die bei einer Änderung des Phasengleichgewichts auftreten.
Aus den Grundlagen der Thermodynamik folgt, dass die erste Ableitung der Gibbs-Energie nach der Temperatur gleich der Entropieänderung des Systems ist. Die Ableitung der Gibbs-Energie nach dem Druck ist gleich der Volumenänderung. Wenn beim Wechsel der Phasen im System die Entropie oder das Volumen einen Bruch erleidet, sich also schlagartig ändert, spricht man von einem Phasenübergang erster Ordnung.
Ferner sind die zweiten Ableitungen der Gibbs-Energie in Bezug auf Temperatur und Druck die Wärmekapazität bzw. der Volumenausdehnungskoeffizient. Geht der Übergang zwischen den Phasen mit einem Sprung in den Werten der angegebenen physikalischen Größen einher, so spricht man von einem Phasenübergang zweiter Ordnung.
Beispiele für Transformationen zwischen Phasen

In der Natur gibt es eine Vielzahl unterschiedlicher Übergänge. Markante Beispiele für Übergänge erster Art im Rahmen dieser Einteilung sind die Prozesse des Schmelzens von Metallen oder die Kondensation von Wasserdampf aus Luft, wenn es zu einem Volumensprung im System kommt.
Wenn wir von Übergängen zweiter Ordnung sprechen, dann sind markante Beispiele die Umwandlung von Eisen von einem magnetischen in einen paramagnetischen Zustand bei einer bestimmten Temperatur768 ºC oder die Umwandlung eines metallischen Leiters in einen supraleitenden Zustand bei Temperaturen nahe dem absoluten Nullpunkt.
Gleichungen, die Übergänge der ersten Art beschreiben
In der Praxis ist es oft notwendig zu wissen, wie sich Temperatur, Druck und aufgenommene (freigesetzte) Energie in einem System verändern, wenn darin Phasenumwandlungen stattfinden. Zu diesem Zweck werden zwei wichtige Gleichungen verwendet. Sie werden basierend auf der Kenntnis der Grundlagen der Thermodynamik erh alten:
- Formel von Clapeyron, die den Zusammenhang zwischen Druck und Temperatur bei Umwandlungen zwischen verschiedenen Phasen herstellt.
- Clausius-Formel, die die absorbierte (freigesetzte) Energie und die Temperatur des Systems während der Umwandlung verknüpft.
Die Verwendung beider Gleichungen dient nicht nur der Ermittlung quantitativer Abhängigkeiten physikalischer Größen, sondern auch der Bestimmung des Vorzeichens der Steigung von Gleichgewichtskurven in Phasendiagrammen.
Gleichung zur Beschreibung von Übergängen zweiter Art

Phasenübergänge 1. und 2. Art werden durch unterschiedliche Gleichungen beschrieben, da die Anwendung der Clausius- und Clausius-Gleichungen für Übergänge zweiter Ordnung zu mathematischen Unsicherheiten führt.
Zur Beschreibung letzterer werden die Ehrenfest-Gleichungen verwendet, die durch Kenntnis der Änderungen der Wärmekapazität und des Volumenausdehnungskoeffizienten während des Umwandlungsprozesses einen Zusammenhang zwischen Druck- und Temperaturänderungen herstellen. Die Ehrenfest-Gleichungen werden verwendet, um Leiter-Supraleiter-Übergänge in Abwesenheit eines Magnetfelds zu beschreiben.
WichtigkeitPhasendiagramme
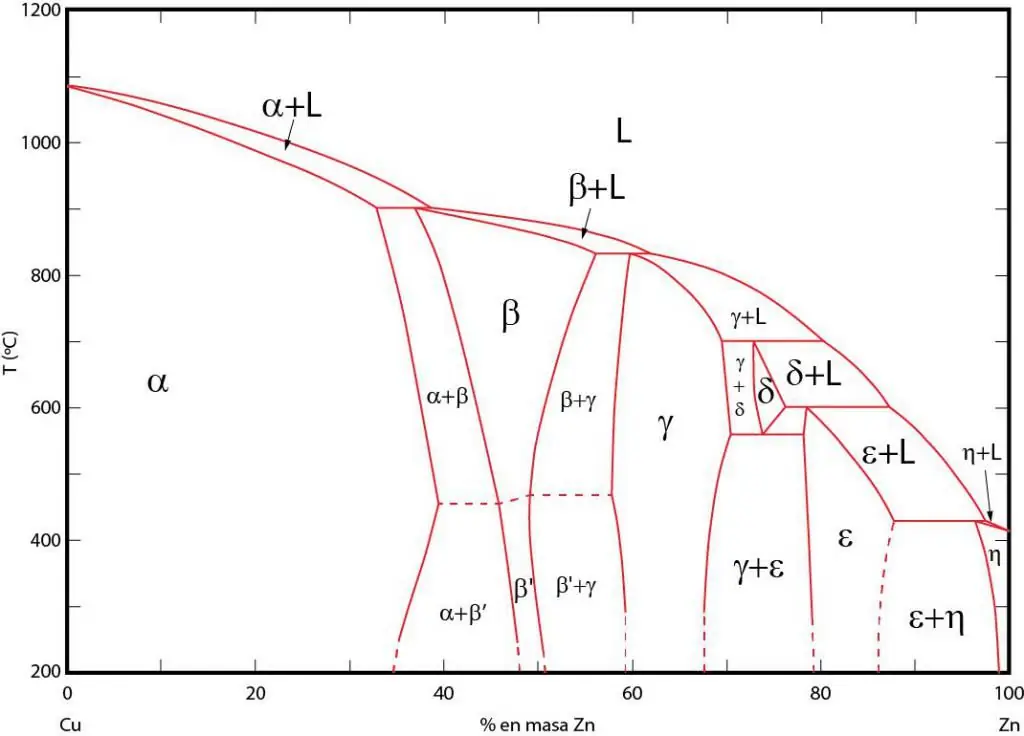
Phasendiagramme sind eine grafische Darstellung von Bereichen, in denen die entsprechenden Phasen im Gleichgewicht vorliegen. Diese Bereiche sind durch Gleichgewichtslinien zwischen den Phasen getrennt. Phasendiagramme P-T (Druck-Temperatur), T-V (Temperatur-Volumen) und P-V (Druck-Volumen) werden häufig verwendet.
Die Bedeutung von Phasendiagrammen liegt darin, dass Sie vorhersagen können, in welcher Phase sich das System befinden wird, wenn sich die äußeren Bedingungen entsprechend ändern. Diese Informationen werden bei der Wärmebehandlung verschiedener Materialien verwendet, um eine Struktur mit gewünschten Eigenschaften zu erh alten.






