Wie Sie wissen, gehört jede physikalische Größe zu einem von zwei Typen, sie ist entweder ein Skalar oder ein Vektor. In diesem Artikel werden wir solche kinematischen Eigenschaften wie Geschwindigkeit und Beschleunigung betrachten und auch zeigen, wohin die Beschleunigungs- und Geschwindigkeitsvektoren gerichtet sind.
Was ist Geschwindigkeit und Beschleunigung?
Beide Größen, die in diesem Absatz erwähnt werden, sind wichtige Eigenschaften jeder Art von Bewegung, egal ob es sich um die Bewegung eines Körpers in einer geraden Linie oder entlang einer gekrümmten Bahn handelt.
Geschwindigkeit ist die Rate, mit der sich Koordinaten im Laufe der Zeit ändern. Mathematisch entspricht dieser Wert der zeitlichen Ableitung der zurückgelegten Strecke, also:
v¯=dl¯/dt.
Hier ist der Vektor l¯ vom Anfangspunkt des Pfades zum Endpunkt gerichtet.
Beschleunigung wiederum ist die Geschwindigkeit, mit der sich die Geschwindigkeit selbst zeitlich ändert. In Form einer Formel kann es so geschrieben werden:
a¯=dv¯/dt.
Offensichtlich wird die zweite Ableitung von genommenVerschiebungsvektor l¯ in der Zeit erh alten wir auch den Wert der Beschleunigung.
Da die Geschwindigkeit in Metern pro Sekunde gemessen wird, wird die Beschleunigung nach dem geschriebenen Ausdruck in Metern pro Sekunde zum Quadrat gemessen.

Wo sind die Beschleunigungs- und Geschwindigkeitsvektoren?
In der Physik ist jede mechanische Bewegung eines Körpers normalerweise durch eine bestimmte Trajektorie gekennzeichnet. Letzteres ist eine imaginäre Kurve, entlang der sich der Körper im Raum bewegt. Beispielsweise sind eine gerade Linie oder ein Kreis Paradebeispiele für übliche Bewegungspfade.
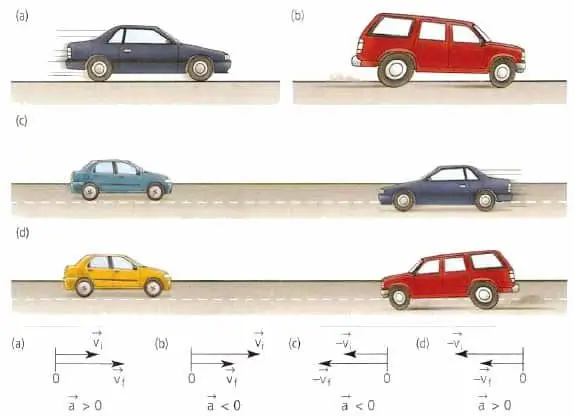
Der Geschwindigkeitsvektor des Körpers ist immer in Bewegungsrichtung gerichtet, egal ob der Körper bremst oder beschleunigt, ob er sich geradlinig oder in einer Kurve bewegt. Geometrisch gesprochen ist der Geschwindigkeitsvektor tangential zu dem Punkt der Bahn gerichtet, in dem sich der Körper gerade befindet.
Der Beschleunigungsvektor eines Material- oder Körperpunktes hat nichts mit Geschwindigkeit zu tun. Dieser Vektor ist in Richtung der Geschwindigkeitsänderung gerichtet. Beispielsweise kann bei einer geradlinigen Bewegung der Wert a¯ in Richtung entweder mit v¯ zusammenfallen oder v¯ entgegengesetzt sein.
Auf den Körper wirkende Kraft und Beschleunigung
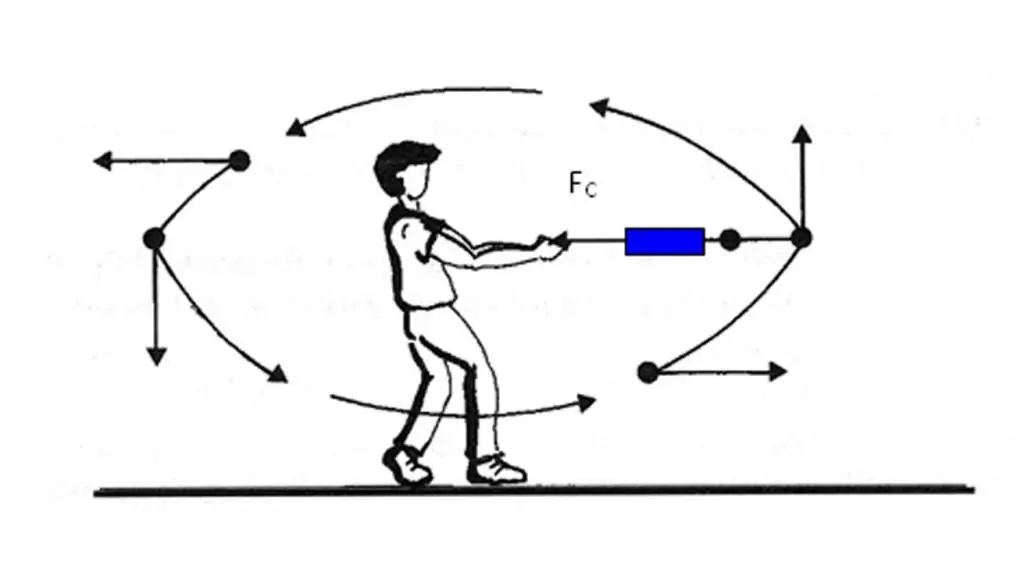
Wir haben herausgefunden, dass der Beschleunigungsvektor des Körpers auf die Änderung des Geschwindigkeitsvektors gerichtet ist. Es ist jedoch nicht immer einfach festzustellen, wie sich die Geschwindigkeit an einem bestimmten Punkt der Trajektorie ändert. Darüber hinaus ist es zum Bestimmen der Geschwindigkeitsänderung erforderlich, die Operation durchzuführenVektorunterschiede. Um diese Schwierigkeiten bei der Bestimmung der Richtung des Vektors a¯ zu vermeiden, gibt es einen anderen Weg, es schnell herauszufinden.
Unten ist Newtons berühmtes und wohlbekanntes Gesetz für jeden Schüler:
F¯=ma¯.
Die Formel zeigt, dass die Ursache der Beschleunigung in Körpern die auf sie wirkende Kraft ist. Da die Masse m ein Skalar ist, haben der Kraftvektor F¯ und der Beschleunigungsvektor a¯ die gleiche Richtung. Diese Tatsache sollte in der Praxis immer dann beachtet und angewendet werden, wenn es darum geht, die Richtung der Größe a¯.
zu bestimmen.
Wirken auf den Körper mehrere unterschiedliche Kräfte, so ist die Richtung des Beschleunigungsvektors gleich dem resultierenden Vektor aller Kräfte.
Kreisbewegung und Beschleunigung
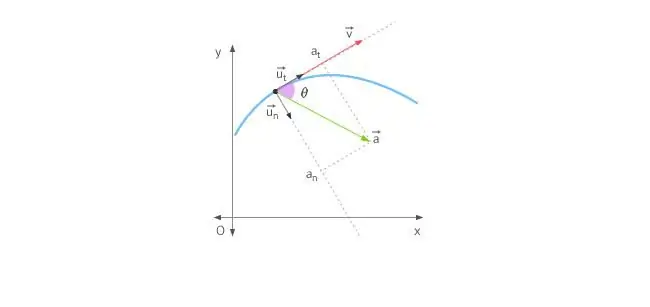
Wenn sich ein Körper in einer geraden Linie bewegt, ist die Beschleunigung entweder nach vorne oder nach hinten gerichtet. Bei einer Kreisbewegung wird die Situation dadurch kompliziert, dass der Geschwindigkeitsvektor ständig seine Richtung ändert. In Anbetracht dessen wird die Gesamtbeschleunigung durch ihre beiden Komponenten bestimmt: Tangential- und Normalbeschleunigung.
Tangentialbeschleunigung ist genauso gerichtet wie der Geschwindigkeitsvektor oder dagegen. Mit anderen Worten, diese Beschleunigungskomponente ist entlang der Tangente an die Trajektorie gerichtet. Die Tangentialbeschleunigung beschreibt die Änderung des Geschwindigkeitsmoduls selbst.
Die Normalbeschleunigung wird entlang der Normalen zum gegebenen Punkt der Trajektorie gerichtet, wobei ihre Krümmung berücksichtigt wird. Im Falle einer kreisförmigen Bewegung gibt der Vektor dieser Komponente anzum Mittelpunkt, das heißt, die Normalbeschleunigung ist entlang des Rotationsradius gerichtet. Diese Komponente wird oft als zentripetal bezeichnet.
Die volle Beschleunigung ist die Summe dieser Komponenten, ihr Vektor kann also beliebig in Bezug auf die Kreislinie gerichtet sein.
Wenn sich der Körper dreht, ohne die lineare Geschwindigkeit zu ändern, dann gibt es nur eine Normalkomponente ungleich Null, sodass der volle Beschleunigungsvektor auf den Mittelpunkt des Kreises gerichtet ist. Beachten Sie, dass dieses Zentrum auch von einer Kraft beeinflusst wird, die den Körper auf seiner Flugbahn hält. Beispielsweise hält die Gravitationskraft der Sonne unsere Erde und andere Planeten auf ihren Bahnen.






