Beschleunigung und Geschwindigkeit sind zwei wichtige kinematische Eigenschaften jeder Art von Bewegung. Kennt man die Abhängigkeit dieser Größen von der Zeit, kann man den zurückgelegten Weg des Körpers berechnen. Dieser Artikel enthält die Antwort auf die Frage, wie man die Beschleunigung findet, wenn man die Geschwindigkeit und Zeit kennt.
Das Konzept von Geschwindigkeit und Beschleunigung
Bevor wir eine Antwort auf die Frage geben, wie man bei Kenntnis von Geschwindigkeit und Zeit die Beschleunigung finden kann, betrachten wir jede der Eigenschaften aus physikalischer Sicht.
Geschwindigkeit ist ein Wert, der die Geschwindigkeit der Änderung von Koordinaten im Raum bestimmt, wenn sich der Körper bewegt. Die Geschwindigkeit wird nach folgender Formel berechnet:
v=dl/dt.
Wobei dl der Weg ist, den der Körper während der Zeit dt zurückgelegt hat. Die Geschwindigkeit richtet sich immer entlang der Tangente im Bewegungspfad.
Bewegung kann entweder zeitlich konstant oder mit variabler Geschwindigkeit erfolgen. Im letzteren Fall spricht man von Beschleunigung. In der Physik bestimmt die Beschleunigung die Änderungsrate von v, die als Formel geschrieben wird:
a=dv/dt.
Diese Gleichheit ist die Antwort auf die Frage nach dem FindenGeschwindigkeitsbeschleunigung. Dazu genügt es, die erste zeitliche Ableitung von v.
zu nehmen.
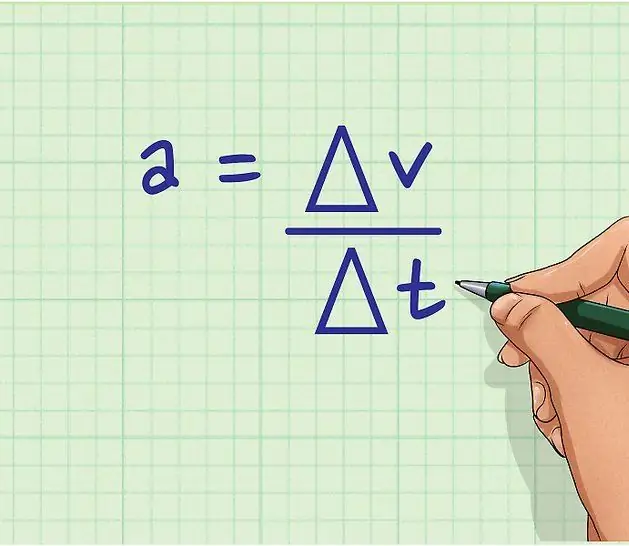
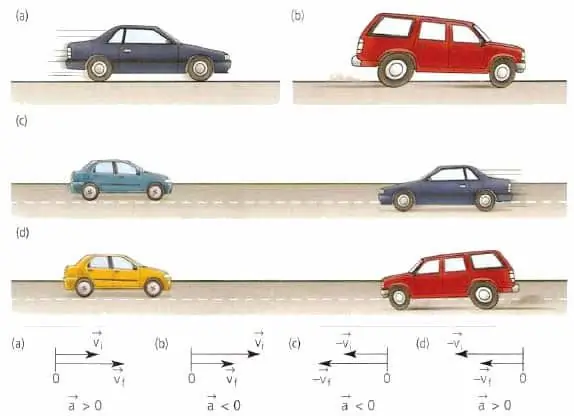
Die Richtung der Beschleunigung fällt mit der Richtung der Differenz der Geschwindigkeitsvektoren zusammen. Bei geradliniger beschleunigter Bewegung sind die Größen a und v in die gleiche Richtung gerichtet.
Wie finde ich die Beschleunigung bei gegebener Geschwindigkeit und Zeit?
Beim Studium der Mechanik betrachtet man zunächst gleichmäßige und gleichmäßig beschleunigte Bewegungsarten entlang einer geraden Bahn. In beiden Fällen sollte das Zeitintervall Δt zur Bestimmung der Beschleunigung gewählt werden. Dann müssen die Werte der Geschwindigkeiten v1 und v2 an den Enden dieses Intervalls bestimmt werden. Die durchschnittliche Beschleunigung ist wie folgt definiert:
a=(v2- v1)/Δt.
Bei gleichförmiger Bewegung bleibt die Geschwindigkeit konstant (v2=v1), also der Wert eines Willens Null sein. Bei gleichmäßig beschleunigter Bewegung ist der Wert a konstant, hängt also nicht vom Zeitintervall Δt in der Formel ab.
Für komplexere Bewegungsfälle, wenn die Geschwindigkeit eine Funktion der Zeit ist, sollten Sie die Formel für a durch die Ableitung verwenden, die im obigen Absatz vorgestellt wurde.
Beispiel zur Problemlösung
Nachdem wir uns mit der Frage beschäftigt haben, wie man die Beschleunigung findet und die Zeit und Geschwindigkeit kennt, werden wir ein einfaches Problem lösen. Angenommen, der Körper, der sich entlang einer bestimmten Bahn bewegt, ändert seine Geschwindigkeit gemäß der folgenden Gleichung:
v=3t2- t + 4.
Wie groß ist die Beschleunigung des Körpers zum Zeitpunkt t=5 Sekunden?
Die Beschleunigung ist die erste Ableitung von v nach der Variablen t, wir haben:
a=dv/dt=6t - 1.
Um die Frage des Problems zu beantworten, sollten Sie den bekannten Wert der Zeit in die resultierende Gleichung einsetzen: a=29 m/c2.






