In der Thermodynamik ist es bei der Untersuchung von Übergängen vom Anfangs- zum Endzustand eines Systems wichtig, den thermischen Effekt des Prozesses zu kennen. Das Konzept der Wärmekapazität ist eng mit diesem Effekt verbunden. In diesem Artikel gehen wir der Frage nach, was man unter der isochoren Wärmekapazität eines Gases versteht.
Ideales Gas
Ein ideales Gas ist ein Gas, dessen Teilchen als materielle Punkte betrachtet werden, das heißt, sie haben keine Dimensionen, aber eine Masse, und bei dem alle innere Energie ausschließlich aus der kinetischen Energie der Bewegung von Molekülen besteht und Atome.
Jedes reale Gas wird idealerweise niemals das beschriebene Modell erfüllen, da seine Teilchen immer noch einige lineare Abmessungen haben und über schwache Van-der-Waals-Bindungen oder chemische Bindungen eines anderen Typs miteinander wechselwirken. Bei niedrigen Drücken und hohen Temperaturen sind die Abstände zwischen Molekülen jedoch groß, und ihre kinetische Energie übersteigt die potentielle Energie um ein Dutzend Mal. All dies ermöglicht es, das ideale Modell für reale Gase mit hoher Genauigkeit anzuwenden.
Innere Energie des Gases
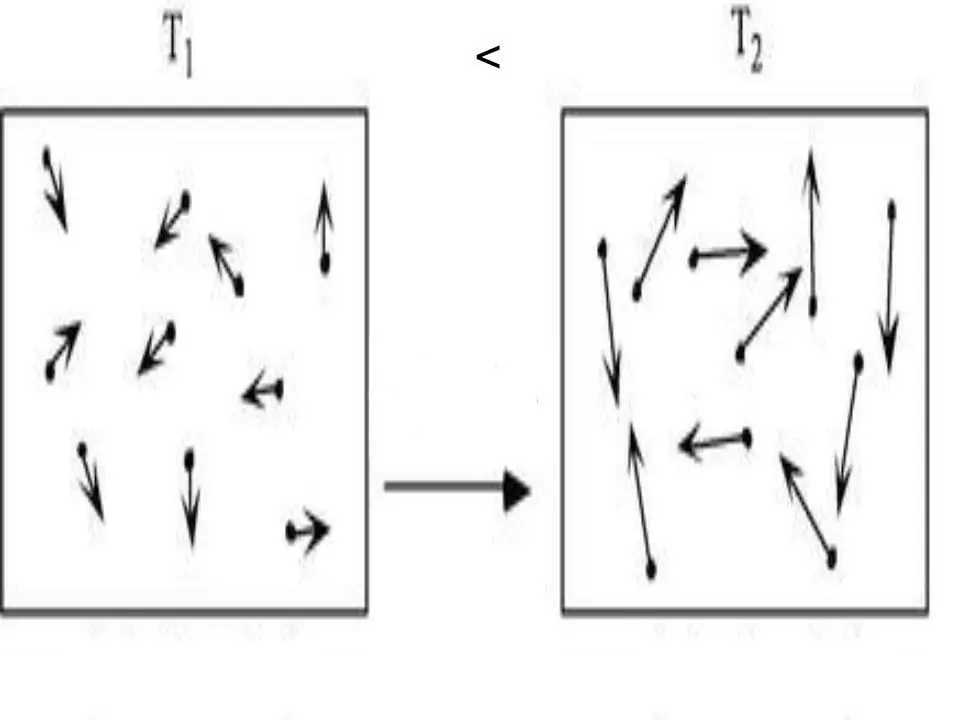
Die innere Energie eines jeden Systems ist eine physikalische Eigenschaft, die gleich der Summe aus potentieller und kinetischer Energie ist. Da bei idealen Gasen die potentielle Energie vernachlässigt werden kann, können wir für sie die Gleichheit schreiben:
U=Ek.
wobei Ek die Energie des kinetischen Systems ist. Unter Verwendung der molekularkinetischen Theorie und der Anwendung der universellen Clapeyron-Mendeleev-Zustandsgleichung ist es nicht schwierig, einen Ausdruck für U zu erh alten. Er wird unten geschrieben:
U=z/2nRT.
Hier sind T, R und n die absolute Temperatur, die Gaskonstante bzw. die Stoffmenge. Der z-Wert ist eine Ganzzahl, die die Anzahl der Freiheitsgrade eines Gasmoleküls angibt.
Isobare und isochore Wärmekapazität
Wärmekapazität ist in der Physik die Wärmemenge, die dem untersuchten System zugeführt werden muss, um es um ein Kelvin zu erwärmen. Auch die umgekehrte Definition gilt, d. h. die Wärmekapazität ist die Wärmemenge, die das System bei Abkühlung um ein Kelvin abgibt.
Der einfachste Weg für ein System ist die Bestimmung der isochoren Wärmekapazität. Darunter versteht man die Wärmekapazität bei konstantem Volumen. Da das System unter solchen Bedingungen keine Arbeit verrichtet, wird die gesamte Energie für die Erhöhung der internen Energiereserven aufgewendet. Bezeichnen wir die isochore Wärmekapazität mit dem Symbol CV, dann können wir schreiben:
dU=CVdT.
Das heißt, die Veränderung der inneren EnergieSystem ist direkt proportional zur Änderung seiner Temperatur. Vergleichen wir diesen Ausdruck mit der im vorigen Absatz geschriebenen Gleichung, so erh alten wir die Formel für CV in einem idealen Gas:
СV=z/2nR.
Dieser Wert ist in der Praxis unpraktisch, da er von der Stoffmenge im System abhängt. Daher wurde das Konzept der spezifischen isochoren Wärmekapazität eingeführt, dh ein Wert, der entweder pro 1 Mol Gas oder pro 1 kg berechnet wird. Bezeichnen wir den ersten Wert mit dem Symbol CV, den zweiten - mit dem Symbol CV m. Für sie können Sie die folgenden Formeln schreiben:
CV=z/2R;
CVm=z/2R/M.
Hier ist M die Molmasse.
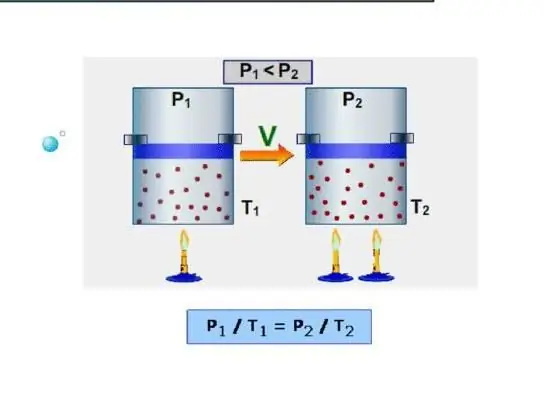
Isobar ist die Wärmekapazität bei Aufrechterh altung eines konstanten Drucks im System. Ein Beispiel für einen solchen Vorgang ist die Expansion von Gas in einem Zylinder unter einem Kolben, wenn dieser erhitzt wird. Im Gegensatz zum isochoren Prozess wird während des isobaren Prozesses die dem System zugeführte Wärme verbraucht, um die innere Energie zu erhöhen und mechanische Arbeit zu verrichten, d.h.:
H=dU + PdV.
Die Enthalpie eines isobaren Prozesses ist das Produkt aus der isobaren Wärmekapazität und der Temperaturänderung im System, also:
H=CPdT.
Betrachten wir die Ausdehnung bei einem konstanten Druck von 1 Mol Gas, dann lautet der erste Hauptsatz der Thermodynamik:
CPdT=CV dT + RdT.
Der letzte Term ergibt sich aus der GleichungClapeyron-Mendelejew. Aus dieser Gleichheit folgt der Zusammenhang zwischen isobaren und isochoren Wärmekapazitäten:
CP=CV + R.
Für ein ideales Gas ist die spezifische molare Wärmekapazität bei konstantem Druck immer um R=8, 314 J/(molK) größer als die entsprechende isochore Kennlinie.
Molekülfreiheitsgrade und Wärmekapazität
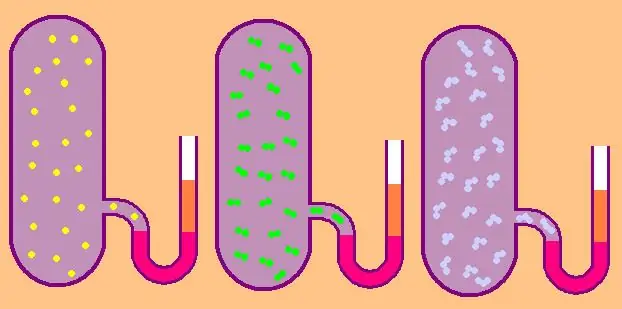
Schreiben wir noch einmal die Formel für die spezifische molare isochore Wärmekapazität:
CV=z/2R.
Im Fall eines einatomigen Gases ist der Wert z=3, da sich Atome im Raum nur in drei unabhängige Richtungen bewegen können.
Wenn wir über ein Gas sprechen, das aus zweiatomigen Molekülen besteht, zum Beispiel Sauerstoff O2 oder Wasserstoff H2, dann Zusätzlich zur Translationsbewegung können sich diese Moleküle noch um zwei zueinander senkrechte Achsen drehen, d.h. z wird gleich 5 sein.
Verwenden Sie für komplexere Moleküle z=6. zur Bestimmung von CV






