Die natürlichen Phänomene und Prozesse um uns herum sind ziemlich komplex. Zu ihrer exakten physikalischen Beschreibung sollte ein umständlicher mathematischer Apparat verwendet und eine Vielzahl signifikanter Faktoren berücksichtigt werden. Um dieses Problem zu vermeiden, werden in der Physik einige vereinfachte Modelle verwendet, die die mathematische Analyse des Prozesses erheblich erleichtern, die Genauigkeit seiner Beschreibung jedoch praktisch nicht beeinträchtigen. Eines davon ist das ideale Gasmodell. Lassen Sie es uns im Artikel genauer betrachten.
Das Konzept eines idealen Gases
Ein ideales Gas ist ein Aggregatzustand eines Stoffes, der aus materiellen Punkten besteht, die nicht miteinander wechselwirken. Lassen Sie uns diese Definition näher erläutern.
Zunächst sprechen wir über materielle Punkte als Objekte, die ein ideales Gas bilden. Das heißt, seine Moleküle und Atome haben keine Größe, sondern eine bestimmte Masse. Es ist mutigeine Annäherung kann unter Berücksichtigung der Tatsache vorgenommen werden, dass in allen realen Gasen bei niedrigen Drücken und hohen Temperaturen der Abstand zwischen Molekülen viel größer ist als ihre linearen Abmessungen.
Zweitens sollten die Moleküle in einem idealen Gas nicht miteinander wechselwirken. In Wirklichkeit gibt es solche Interaktionen immer. So erfahren sogar Atome von Edelgasen eine Dipol-Dipol-Anziehung. Mit anderen Worten, es liegen Van-der-Waals-Wechselwirkungen vor. Im Vergleich zur kinetischen Energie der Rotation und Translation von Molekülen sind diese Wechselwirkungen jedoch so gering, dass sie die Eigenschaften von Gasen nicht beeinflussen. Daher können sie bei der Lösung praktischer Probleme nicht berücksichtigt werden.
Es ist wichtig zu beachten, dass nicht alle Gase, in denen die Dichte niedrig und die Temperatur hoch ist, als ideal angesehen werden können. Neben Van-der-Waals-Wechselwirkungen gibt es noch andere, stärkere Arten von Bindungen, beispielsweise Wasserstoffbrückenbindungen zwischen H2O-Molekülen, die zu einer groben Verletzung der Gasidealitätsbedingungen führen. Aus diesem Grund ist Wasserdampf kein ideales Gas, Luft aber schon.
Physikalisches Modell eines idealen Gases
Dieses Modell kann wie folgt dargestellt werden: Angenommen, das Gassystem enthält N Teilchen. Dies können Atome und Moleküle verschiedener Chemikalien und Elemente sein. Die Anzahl der N-Teilchen ist groß, daher wird üblicherweise die Einheit "Mol" verwendet, um sie zu beschreiben (1 Mol entspricht der Zahl von Avogadro). Sie bewegen sich alle in einem Volumen V. Teilchenbewegungensind chaotisch und unabhängig voneinander. Jeder von ihnen hat eine bestimmte Geschwindigkeit v und bewegt sich auf einer geraden Bahn.
Theoretisch ist die Kollisionswahrscheinlichkeit zwischen Partikeln fast null, da ihre Größe im Vergleich zu den Abständen zwischen den Partikeln klein ist. Kommt es jedoch zu einer solchen Kollision, dann ist sie absolut elastisch. Im letzteren Fall bleiben der Gesamtimpuls der Teilchen und ihre kinetische Energie erh alten.
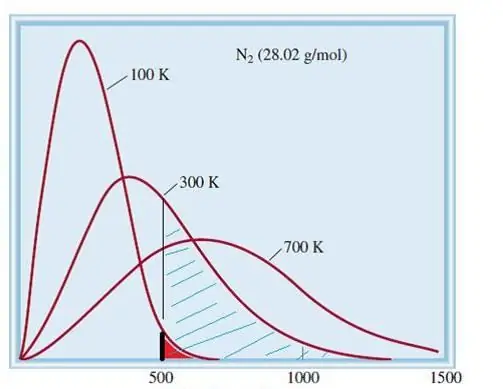
Das betrachtete Modell idealer Gase ist ein klassisches System mit einer riesigen Anzahl von Elementen. Daher gehorchen Geschwindigkeit und Energie der Teilchen darin der statistischen Verteilung von Maxwell-Boltzmann. Einige Partikel haben niedrige Geschwindigkeiten, während andere hohe Geschwindigkeiten haben. In diesem Fall gibt es eine bestimmte enge Geschwindigkeitsbegrenzung, in der die wahrscheinlichsten Werte dieser Größe liegen. Die Geschwindigkeitsverteilung von Stickstoffmolekülen ist unten schematisch dargestellt.
Kinetische Gastheorie
Das oben beschriebene Modell idealer Gase bestimmt eindeutig die Eigenschaften von Gasen. Dieses Modell wurde erstmals 1738 von Daniel Bernoulli vorgeschlagen.

In der Folge wurde es von August Kroenig, Rudolf Clausius, Mikhail Lomonosov, James Maxwell, Ludwig Boltzmann, Marian Smoluchowski und anderen Wissenschaftlern bis zu seinem heutigen Stand weiterentwickelt.
Die kinetische Theorie flüssiger Substanzen, auf deren Grundlage das ideale Gasmodell aufgebaut ist, erklärt zwei wichtige makroskopische Eigenschaften des Systems anhand seines mikroskopischen Verh altens:
- Der Druck in Gasen ist das Ergebnis der Kollision von Partikeln mit den Gefäßwänden.
- Die Temperatur im System ist das Ergebnis der Manifestation der ständigen Bewegung von Molekülen und Atomen.
Erweitern wir beide Schlussfolgerungen der kinetischen Theorie.
Gasdruck
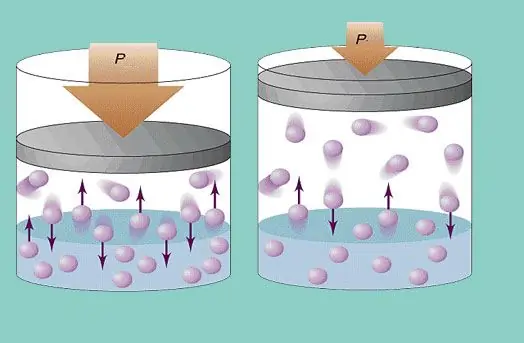
Das Modell des idealen Gases geht von einer ständigen chaotischen Bewegung der Teilchen im System und ihrer ständigen Kollision mit den Gefäßwänden aus. Jede solche Kollision wird als absolut elastisch betrachtet. Die Partikelmasse ist klein (≈10-27-10-25 kg). Daher kann es bei einem Aufprall nicht viel Druck aufbauen. Trotzdem ist die Zahl der Teilchen und damit die Zahl der Kollisionen enorm (≈1023). Außerdem beträgt die mittlere quadratische Geschwindigkeit der Elemente bei Raumtemperatur mehrere hundert Meter pro Sekunde. All dies führt zur Erzeugung eines beträchtlichen Drucks auf die Gefäßwände. Sie kann mit folgender Formel berechnet werden:
P=Nmvcp2 / (3V),
wobei vcp die mittlere quadratische Geschwindigkeit ist, m die Teilchenmasse ist.
Absolute Temperatur
Nach dem idealen Gasmodell wird die Temperatur eindeutig durch die durchschnittliche kinetische Energie eines Moleküls oder Atoms im untersuchten System bestimmt. Sie können den folgenden Ausdruck schreiben, der kinetische Energie und absolute Temperatur für ein ideales Gas in Beziehung setzt:
mvcp2 / 2=3 / 2kB T.
Hier ist kB die Boltzmann-Konstante. Aus dieser Gleichheit erh alten wir:
T=m vcp2 / (3kB).
Universelle Zustandsgleichung
Wenn wir die obigen Ausdrücke für absoluten Druck P und absolute Temperatur T kombinieren, können wir die folgende Gleichung schreiben:
PV=nRT.
Hier ist n die Stoffmenge in Mol, R die von D. I. Mendeleev eingeführte Gaskonstante. Dieser Ausdruck ist die wichtigste Gleichung in der Theorie idealer Gase, da er drei thermodynamische Parameter (V, P, T) kombiniert und nicht von den chemischen Eigenschaften des Gassystems abhängt.

Die universelle Gleichung wurde erstmals im 19. Jahrhundert von dem französischen Physiker Emile Clapeyron experimentell hergeleitet und dann von dem russischen Chemiker Mendeleev in ihre moderne Form gebracht, weshalb sie heute die Namen dieser Wissenschaftler trägt.






