Die Thermodynamik des gasförmigen Aggregatzustands der Materie ist ein wichtiger Zweig der Physik, der das thermodynamische Gleichgewicht und quasistatische Übergänge in Systemen untersucht. Das Hauptmodell, auf dem Vorhersagen über das Verh alten von Systemen basieren, ist das ideale Gasmodell. Mit seiner Verwendung wurde die Mendeleev-Clapeyron-Gleichung erh alten. Betrachten Sie es im Artikel.
Ideales Gas
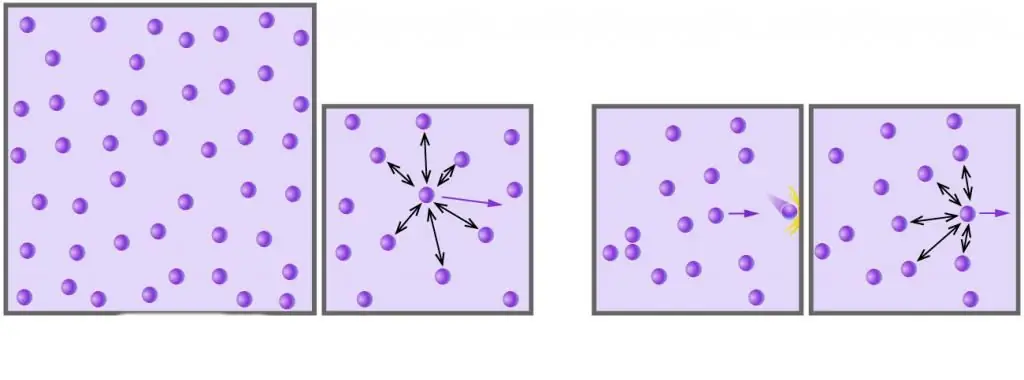
Wie Sie wissen, bestehen alle realen Gase aus Molekülen oder Atomen, deren Abstände im Vergleich zu ihrer Größe bei niedrigen Drücken zu groß sind. Darüber hinaus übersteigt die kinetische Energie von Molekülen bei hohen Temperaturen im absoluten Maßstab ihre potentielle Energie, die mit schwachen Dipol-Dipol-Wechselwirkungen verbunden ist (wenn zusätzlich zu diesen Wechselwirkungen andere Arten chemischer Bindungen vorhanden sind, z. B. ionische oder Wasserstoff, dann leisten sie einen wesentlichen Beitrag zum Potentialanteil der systeminternen Energie).
WegenBei vielen realen Gasen unter nahezu normalen Bedingungen kann man ihre internen Wechselwirkungen und Partikelgrößen vernachlässigen. Diese beiden Hauptannäherungen bilden das ideale Gasmodell.
Mendeleevs Gleichung in der Physik

Es ist korrekter und fairer, diese Gleichung das Clapeyron-Mendeleev-Gesetz zu nennen. Tatsache ist, dass es erstmals 1834 vom französischen Ingenieur Emile Clapeyron aufgezeichnet wurde. Er tat dies, indem er die Anfang des 19. Jahrhunderts entdeckten Gasgesetze von Boyle-Mariotte, Gay-Lussac und Charles analysierte.
Das Verdienst des russischen Chemikers Dmitri Mendelejew liegt darin, dass er der Gleichung eine moderne und einfach zu handhabende mathematische Form gegeben hat. Insbesondere führte Mendelejew in die Gleichung eine Konstante für alle Gase R=8, 314 J/(molK) ein. Clapeyron selbst hat eine Reihe empirischer Konstanten verwendet, die den Berechnungsprozess erschweren.
Die Mendeleev-Clapeyron-Gleichung wird wie folgt geschrieben:
PV=nRT.
Diese Gleichheit bedeutet, dass das Produkt aus Druck P und Volumen V auf der linken Seite des Ausdrucks immer proportional zum Produkt aus absoluter Temperatur T und Stoffmenge n auf der linken Seite ist.
Der zu untersuchende Ausdruck ermöglicht es Ihnen, jedes Gasgesetz zu erh alten, wenn Sie zwei seiner vier Parameter festlegen. Bei Isoprozessen werden geschlossene Systeme untersucht, in denen kein Stoffaustausch mit der Umgebung stattfindet (n=const). Diese Prozesse sind durch einen einzigen festen thermodynamischen Parameter (T, P oder V) gekennzeichnet.

Beispielaufgabe
Nun wollen wir das Problem der Mendelejew-Clapeyron-Gleichung lösen. Es ist bekannt, dass sich Sauerstoff mit einem Gewicht von 500 Gramm in einer Flasche mit einem Volumen von 100 Litern bei einem Druck von 2 Atmosphären befindet. Wie hoch ist die Temperatur im Ballon, wenn sich das System im thermodynamischen Gleichgewicht befindet.
Denken Sie daran, dass laut Definition die Menge eines Stoffes nach folgender Formel berechnet wird:
n=m/M.
Wo m die Masse aller Teilchen des Systems ist, ist M ihre durchschnittliche Molmasse. Diese Gleichheit ermöglicht es uns, die Mendeleev-Gleichung in die folgende Form umzuschreiben:
PV=mRT/M.
Wo wir die Arbeitsformel für diese Aufgabe bekommen:
T=PVM/(mR).
Es bleibt noch, alle Größen in SI-Einheiten umzuwandeln und sie in diesen Ausdruck einzusetzen:
T=21013250, 10, 032/(0, 58, 314)=156 K.
Berechnete Temperatur ist -117 oC. Obwohl Sauerstoff bei dieser Temperatur noch gasförmig ist (er kondensiert bei -182,96 oC), kann das ideale Gasmodell unter solchen Bedingungen nur verwendet werden, um eine qualitative Schätzung des berechneten Werts zu erh alten.






